Предмет: Математика,
автор: solovey567
Розв’язати систему рівнянь з двома змінними
Приложения:
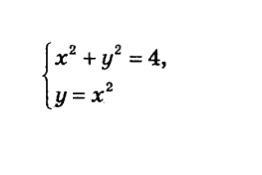
Ответы
Автор ответа:
0
Ответ:
Решения системы:
Пошаговое объяснение:
не является корнем систему уравнений, так как
, то
.
Решения системы:
gthtvjufpfyfvb6:
https://znanija.com/task/51592646
Похожие вопросы
Предмет: Геометрия,
автор: glasha121221
Предмет: Математика,
автор: katerynamokrenets11
Предмет: Математика,
автор: katerynamokrenets11
Предмет: Математика,
автор: knyshksenya403
Предмет: Українська література,
автор: angelisha0