Question

Помогите пожалуйста !!​

Answer 1

Ответ:

1) Площадь криволинейной трапеции равна $\boldsymbol{\displaystyle \frac{\sqrt[3]{81}}{4} -3\sqrt[3]{3} + 6}$ квадратных единиц

2) Площадь криволинейной трапеции равна 2 квадратные единицы

Пошаговое объяснение:

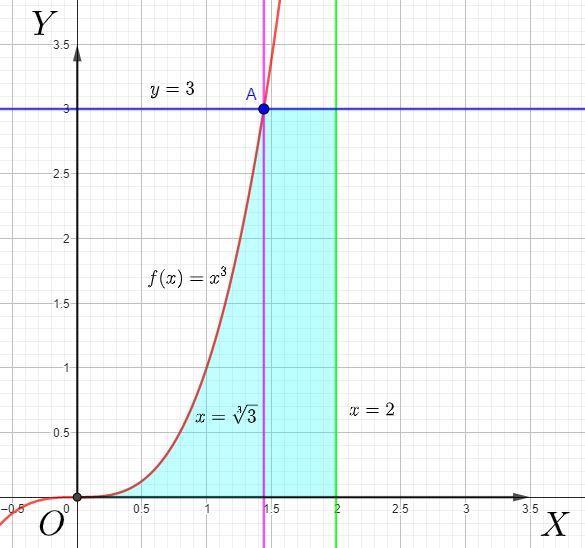
1)

Криволинейная трапеция ограниченна линиями:

$y = 0$

$y = 3$

$x = 2$

$f(x) = x^{3}$

Пусть точка A - точка пересечения кривой $f(x) = x^{3}$ и $y = 3$:

$x^{3} = 3 \Longrightarrow x = \sqrt[3]{3}$

Таким образом прямая $x = \sqrt[3]{3}$ разбивает криволинейную трапеция на две части (см.рисунок) , тогда согласно геометрическому смыслу определенного интеграла:

$\displaystyle S = \int\limits^{\sqrt[3]{3} }_{0} {x^{3}} \, dx +\int\limits^{2}_{\sqrt[3]{3} } {3} \, dx = \frac{x^{4}}{4} \bigg |_{0}^{\sqrt[3]{3} } + 3\int\limits^{2}_{\sqrt[3]{3} }dx = \frac{1}{4} \bigg((\sqrt[3]{3})^{4} - 0^{4} \bigg) + 3x \bigg |^{2}_{\sqrt[3]{3} } =$

$\displaystyle = \frac{1}{4} \bigg(\sqrt[3]{81} - 0\bigg) + 3(2 - \sqrt[3]{3})=\frac{\sqrt[3]{81}}{4} -3\sqrt[3]{3} + 6 \approx 2,8$ квадратных единиц.

2)

Согласно  геометрическому смыслу определенного интеграла:

$\displaystyle S = \int\limits^{\pi}_{0} {\sin x} \, dx = - \cos x \bigg |_{0}^{\pi} =-(\cos \pi - \cos 0) = -(-1 - 1) = 1 + 1 = 2$ квадратных единиц.