Предмет: Математика,
автор: elzamin2004
Найти ответ .............
Приложения:
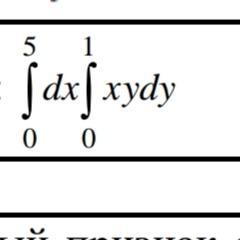
Ответы
Автор ответа:
1
Ответ:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: kuharvsevolod
Предмет: Математика,
автор: danicschuka
Предмет: Математика,
автор: spavlovska78
Предмет: Алгебра,
автор: anciferiva