Предмет: Математика,
автор: maryiily
Прошу помогите. Найти общее решение дифференциального уравнения
Приложения:
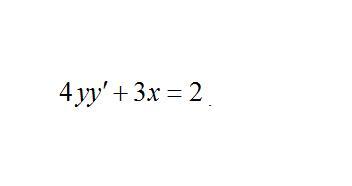
Ответы
Автор ответа:
1
Ответ:
Решение дифференциального уравнения:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
- общий интеграл дифференциального уравнения
maryiily:
Спасибо!
Похожие вопросы
Предмет: Геометрия,
автор: LIBERHack
Предмет: Другие предметы,
автор: sghhajjhnz
Предмет: Математика,
автор: amia112
Предмет: Математика,
автор: alongerk92
Предмет: Русский язык,
автор: lusin841