Предмет: Математика,
автор: maryiily
Помогите пожалуйста! Найти производную функции, заданной параметрически
Приложения:
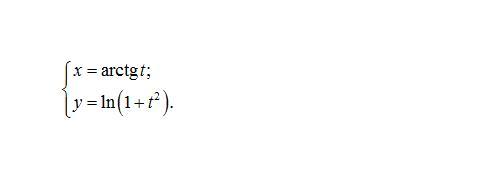
Ответы
Автор ответа:
1
Решение.
Производная функции , заданной параметрически.
maryiily:
Спасибо за помощь!
Похожие вопросы
Предмет: Литература,
автор: aytenc511
Предмет: Физика,
автор: hiwkwv
Предмет: Алгебра,
автор: lol4iktiken
Предмет: Русский язык,
автор: WolfgangSchmerz