Розв'яжіть графічно систему рівнянь. Завдання на малюнку.
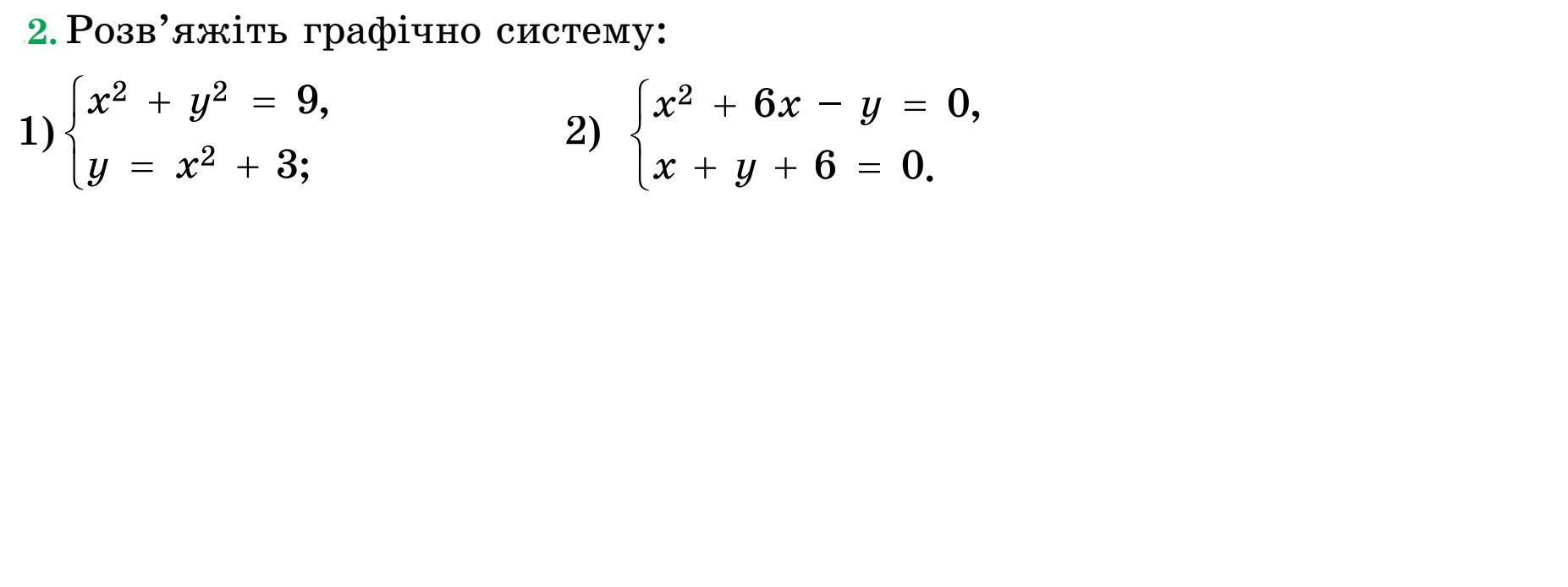
Ответы
Ответ:
1. (0; 3)
2. (-6; 0); (-1; -5).
Объяснение:
Решить систему графически.
1.
Чтобы решить систему графически, надо построить графики. Координаты точек пересечения и будут решениями данной системы.
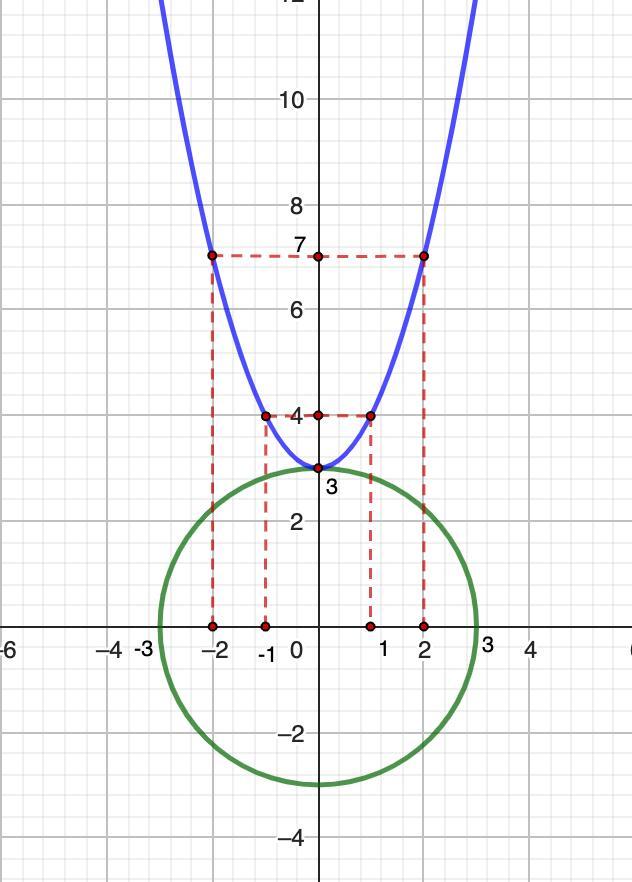
1) х² + у² = 3²
- уравнение окружности с началом координат в точке (0; 0) и радиусом 3 ед.
2) у = х² + 3
-квадратичная функция, график парабола, ветви вверх.
Координаты вершины (0; 3)
Дополнительные точки:
Строим графики.
Они имеют одну точку пересечения с координатими (0; 3)
Ответ: (0; 3)
2.
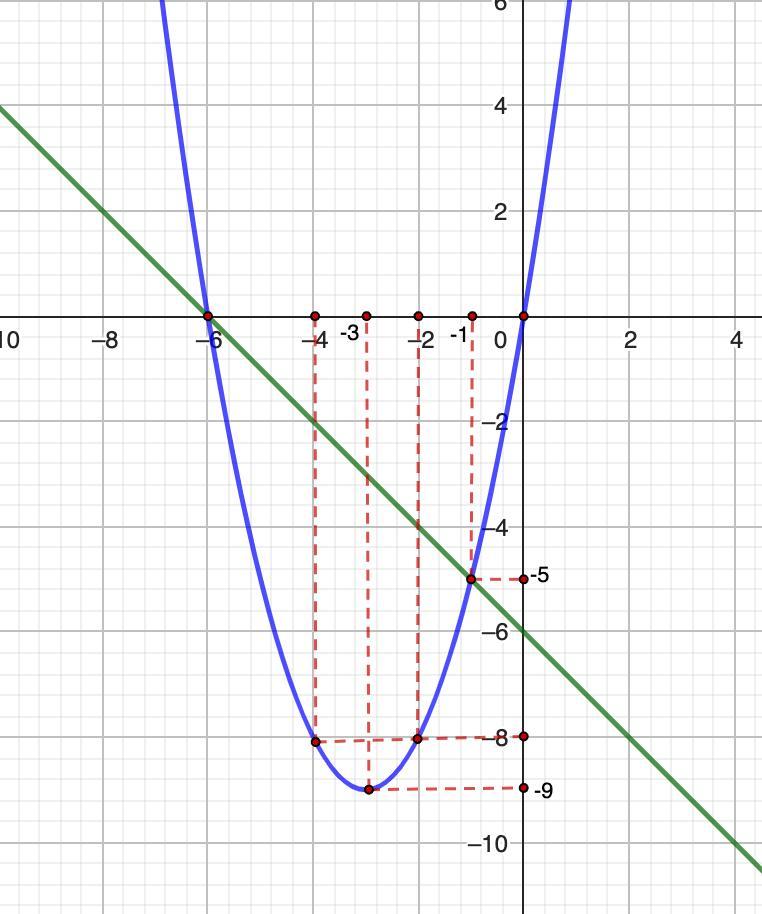
1) x² + 6x - y=0 ⇒ y = x² + 6x
- квадратичная функция, график - парабола, ветви вверх.
Вершина:
Дополнительные точки:
2) x + y + 6 = 0 ⇒ y = -x - 6
- линейная функция, график прямая.
Достаточно двух точек:
Строим графики.
Точки пересечения имеют координаты (-6; 0) и (-1; -5)
Ответ: (-6; 0); (-1; -5).