Question

помогите пожалуйста ​

Answer 1

Ответ:

Площадь треугольника АВС равна 240 см².

Объяснение:

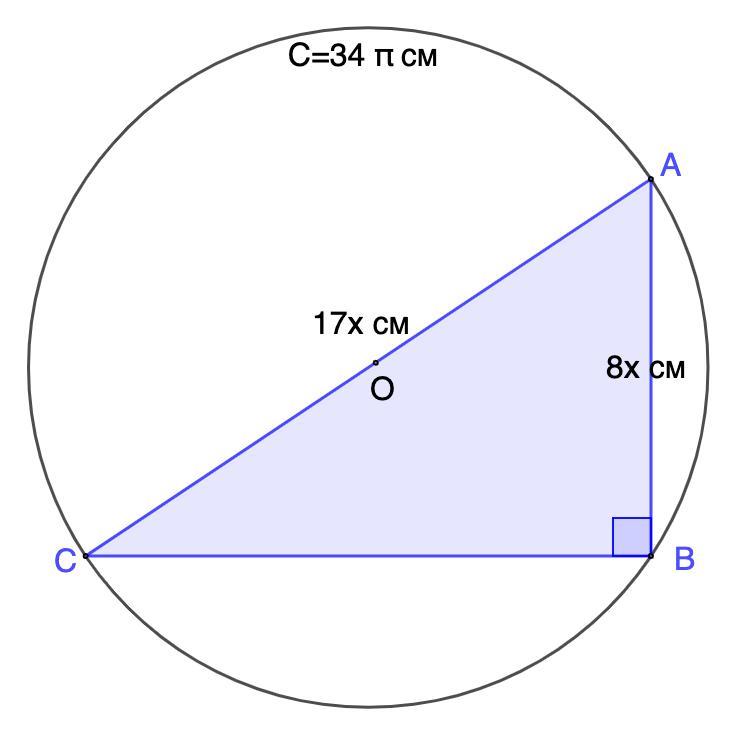
3. Дано ΔАВС: ∠B = 90°, катет и гипотенуза относятся как 8:17. Найти площадь этого треугольника, если длина окружности, описанного около треугольника, равна 34π см.

Дано: ΔАВС - прямоугольный (∠В = 90°)

АВ : АС = 8 : 17.

Окр.(О) - описанная; С = 34π см.

Найти: S(ABC)

Решение:

АВ : АС = 8 : 17

Пусть АВ = 8х см; тогда АС = 17х см.

Окр.(О) - описанная.

• Вписанный прямой угол опирается на диаметр.

⇒ АС - гипотенуза ΔАВС является диаметром Окр.(О).

Формула длины окружности:

C = 2πR = πd ,

где d - диаметр.

34π = π · 17х

17х = 34

х = 2

⇒ АС = 17х = 34 (см); АВ = 8х = 16 (см)

По теореме Пифагора найдем ВС:

ВС² = АС² - АВ² = 1156 - 256 = 900   ⇒   ВС = √900 = 30 (см)

• Площадь прямоугольного треугольника равна половине произведения катетов.

$\displaystyle \bf S(ABC)=\frac{1}{2}\cdot CB\cdot AB=\frac{1}{2}\cdot 30 \cdot 16 = 240$   (см²)

Площадь треугольника АВС равна 240 см².