Предмет: Математика,
автор: petrenkoveronika2007
Помогите пожалуйста! даю 30 баллов!
Приложения:
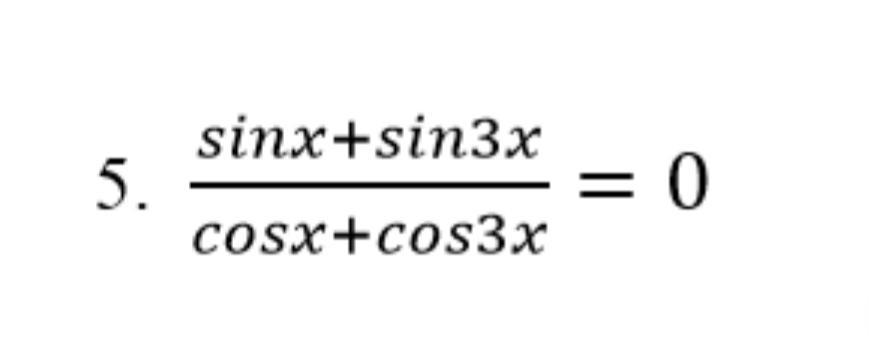
Ответы
Автор ответа:
3
Ответ.
Применяем формулы суммы синусов и суммы косинусов .
.
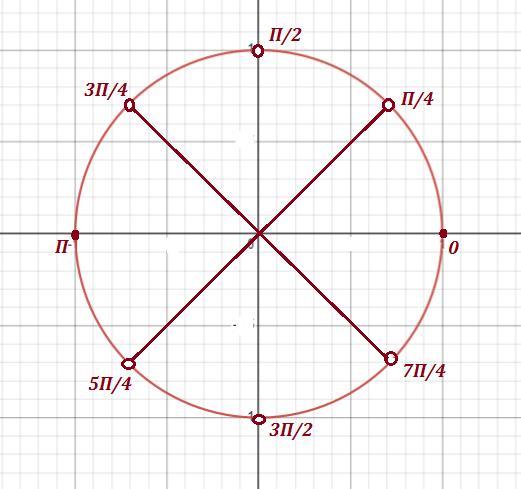
ОДЗ:
Учитывая ОДЗ получим окончательный ответ.
Ответ:
Приложения:
Похожие вопросы
Предмет: География,
автор: Miroslava696
Предмет: Литература,
автор: Flower3456666
Предмет: Окружающий мир,
автор: sofiazavidnak441
Предмет: Математика,
автор: barevgeniy