Question

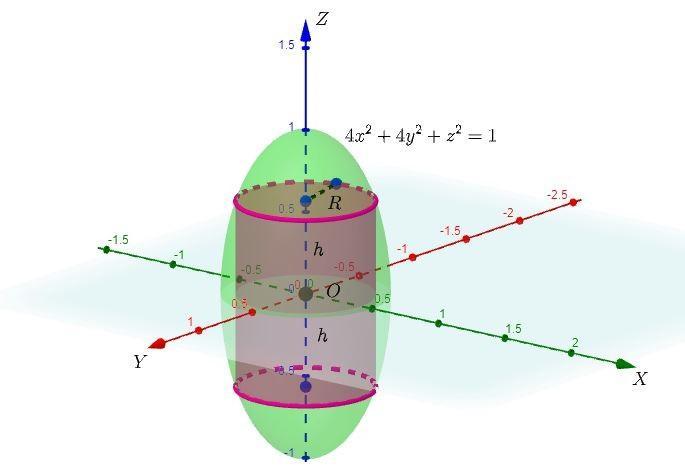
Найти размеры (высоту H и радиус R) прямого кругового цилиндра наибольшего объёма, ось которого совпадает с осью OZ, а сам цилиндр вписан в эллипсоид
$4x^2 +4y^2 + z^2 = 1$

Answer 1

Ответ:

Высота прямого кругового цилиндра наибольшего объёма

равна $\boldsymbol{\dfrac{2\sqrt{3}}{3}}$, а радиус - $\boldsymbol{\dfrac{\sqrt{6} }{6}}$.

$\boldsymbol{\boxed{H =\dfrac{2\sqrt{3}}{3}}}$

$\boldsymbol{\boxed{R =\dfrac{\sqrt{6} }{6}}}$

Пошаговое объяснение:

Рассмотрим уравнение эллипсоида $4x^{2} + 4y^{2} + z^{2} = 1$.

Перепишем данное уравнение в следующем виде:

$4x^{2} + 4y^{2} + z^{2} = 1$

$4x^{2} + 4y^{2} = 1 - z^{2}|:4$

$x^{2} + y^{2} = \dfrac{1 - z^{2}}{4}$

Можно сказать, что эллипсоид задается как множество окружностей, которое находятся параллельно плоскости $XOY$ и их радиус зависит от высоты по данному уравнению $x^{2} + y^{2} = \dfrac{1 - z^{2}}{4}$. Так как в уравнении эллипсоида $z$ в четной степени, то точки эллипсоида симметричны относительно плоскости $XOY$, тогда и вписанный в эллипсоид прямой цилиндр будет симметричен относительно плоскости $XOY$. Таким образом достаточно найти прямой цилиндр максимального объема вписанный в часть  эллипсоида при $z \in (0;1)$. Так как эллипсоид задается как множество окружностей, которое находятся параллельно плоскости $XOY$ и их радиус зависит от высоты по данному уравнению $x^{2} + y^{2} = \dfrac{1 - z^{2}}{4}$, то высота цилиндра $h = z$ и $x^{2} + y^{2} = R^{2}$ - уравнение окружности, то есть $R^{2} = \dfrac{1 - z^{2}}{4}$. Составим функцию которая описывает объем эллипсоида от его радиуса и высоты:

$V = \pi hR^{2}$, то есть $V(z) = \pi z \cdot \dfrac{1 - z^{2}}{4} = \dfrac{\pi }{4} \bigg(z - z^{3} \bigg)$, где $V(z) \ -$ вещественнозначная функция.

Продифференцируем функцию $V(z):$

$V'(z) = \Bigg( \dfrac{\pi }{4} \bigg(z - z^{3} \bigg) \Bigg)' = \dfrac{\pi }{4} \bigg(1 - 3z^{2} \bigg)$

Экстремумы функции $V(z):$

$V'(z) = 0$

$\dfrac{\pi }{4} \bigg(1 - 3z^{2} \bigg) = 0 \bigg | \cdot \dfrac{4}{\pi}$

$1 - 3z^{2} = 0$

$3z^{2} = 1|:3$

$z^{2} = \dfrac{1}{3}$

$\sqrt{ z^{2} }= \sqrt{ \dfrac{1}{3} }$

$|z| = \dfrac{1}{\sqrt{3} }$, так как $z \in (0;1)$, то $z = \dfrac{1}{\sqrt{3} } = \dfrac{\sqrt{3} }{\sqrt{3} \cdot \sqrt{3}} = \dfrac{\sqrt{3}}{3}$.

Вторая производная функции $V(z):$

$V''(z) =(V'(z))' = \Bigg( \dfrac{\pi }{4} \bigg(1 - 3z^{2} \bigg) \Bigg )' = -\dfrac{6\pi z }{4} = -\dfrac{3\pi z }{2}$

$V''\bigg (\dfrac{\sqrt{3}}{3} \bigg) = -\dfrac{3\pi }{2} \cdot \dfrac{\sqrt{3}}{3} = -\dfrac{\pi \sqrt{3} }{2} < 0$.

Так как $V''\bigg (\dfrac{\sqrt{3}}{3} \bigg) < 0$ и $V'\bigg (\dfrac{\sqrt{3}}{3} \bigg) = 0$, то точка $z = \dfrac{\sqrt{3}}{3}$ - максимум функции $V(z)$.

Так как вписанный в эллипсоид прямой цилиндр будет симметричен относительно плоскости $XOY$, то его высота также симметрична относительно плоскости $XOY$, следовательно $H = 2h = \dfrac{2\sqrt{3}}{3}$.

Радиус окружности прямого цилиндра:

$R^{2} = \dfrac{1 - z^{2}}{4} \Longrightarrow R = \sqrt{\dfrac{1 - z^{2}}{4}} = \sqrt{\dfrac{1 - \bigg (\dfrac{1}{\sqrt{3} } \bigg )^{2}}{4}} = \dfrac{\sqrt{1 - \dfrac{1}{3} } }{\sqrt{4} } =\dfrac{\sqrt{\dfrac{3-1}{3} } }{2} =$

$= \dfrac{\dfrac{\sqrt{2} }{\sqrt{3} } }{\dfrac{2}{1} } = \dfrac{\sqrt{2} }{2\sqrt{3} }= \dfrac{\sqrt{2} \cdot \sqrt{3}}{2\sqrt{3} \cdot \sqrt{3} } = \dfrac{\sqrt{6} }{6}$.