С помощью производной иследовать график функции y=e1/2-x
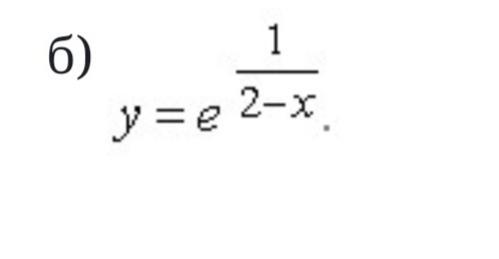
Ответы
Ответ:
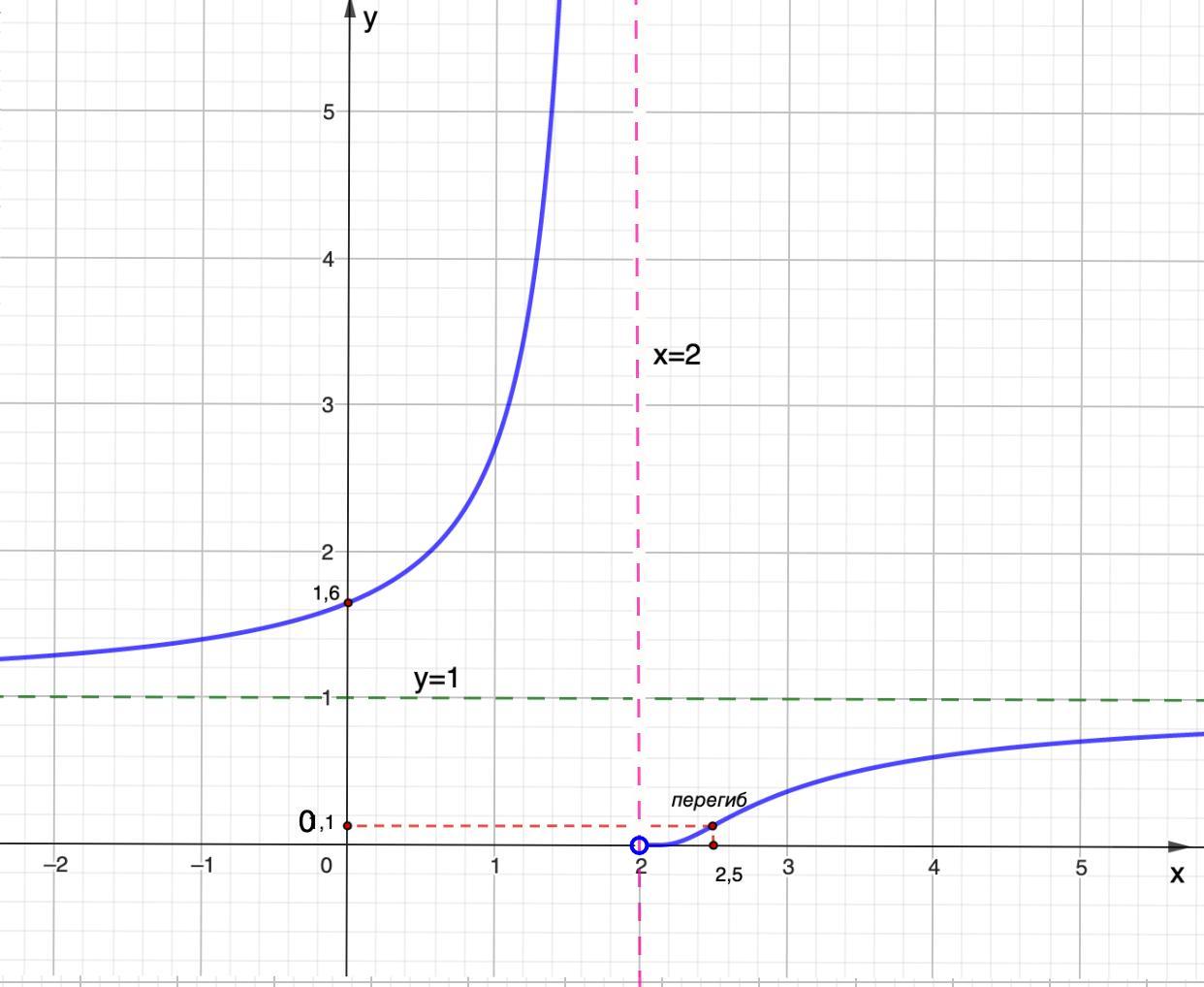
1. D(y) = (-∞; 2)∪(2; +∞)
2. функция не является четной или нечетной
3. ось Ох не пересекает; Ось Оу график пересекает в точке (0; 1,6)
4. x = 2 - вертикальная асимптота.
y = 1 -горизонтальная асимптота.
5. Функция возрастает на промежутках: (-∞; 2); (2; +∞).
6. Функция вогнута на промежутках: (-∞; 2); (2; 2,5]
Выпукла на промежутке: [2,5; +∞)
В точке х = 2,5 - перегиб.
Пошаговое объяснение:
Исследовать функцию и построить график:
1. Область определения функции.
2 - х ≠ 0 ⇒ х ≠ 2
D(y) = (-∞; 2)∪(2; +∞)
2. Четность, нечетность.
- Если f(-x) = f(x), то функция четная, если f(-x) = -f(x) - нечетная.
y(-x) ≠ y(x) ≠ -y(x) ⇒ функция не является четной или нечетной, то есть общего вида.
3. Пересечение с осями.
Так как > 0, то график ось Ох не пересекает и расположен выше оси Ох.
Пересечение с Оу ⇒ х = 0
Ось Оу график пересекает в точке (0; 1,6)
4. Асимптоты.
Вертикальные:
x = 2 - вертикальная асимптота.
Наклонная асимптота y = kx + b.
y = 1 - горизонтальная асимптота.
5. Возрастание, убывание.
Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.
Если "+" - функция возрастает, если "-" - функция убывает.
Числитель и знаменатель положительны, значит функция возрастает на всей области определения.
Критическая точка х = 2
Функция возрастает на промежутках: (-∞; 2); (2; +∞).
Точек экстремумов нет.
6. Выпуклость, вогнутость.
Найдем производную второго порядка и приравняем к нулю. Найдем корни. Отметим их на числовой оси и определим знаки второй производной на промежутках.
Не забываем про точку х ≠ 2.
- Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.
Функция вогнута на промежутках: (-∞; 2); (2; 2,5]
Выпукла на промежутке: [2,5; +∞)
В точке х = 2,5 вторая производная меняет знак ⇒ это точка перегиба.
у(2,5) ≈ 0,1
Строим график.