Предмет: Алгебра,
автор: yuliasidorenko2826
Знайти область визначення функції
Приложения:
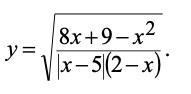
Ответы
Автор ответа:
1
Ответ:
D(y) = [-1; 2) ∪ [9; +∞)
Объяснение:
Найти область определения функции:
Надо знать:
- Подкоренное выражение неотрицательно.
- На ноль делить нельзя.
1.
|x - 5|(2 - x) ≠ 0
х ≠ 5; х ≠ 2
2.
Решим методом интервалов.
Сначала найдем корни уравнения:
Отметим эти точки на числовой оси, не забываем про точки, в которых функция не определена. Найдем знаки на промежутках.
Для этого берем любое значение х на промежутке, подставляем в функцию и смотрим, положительное или отрицательное она примет.
Так как у нас знак ≥, то выбираем промежутки со знаком "+".
⇒ D(y) = [-1; 2) ∪ [9; +∞)
Похожие вопросы
Предмет: География,
автор: dimon0999
Предмет: Українська мова,
автор: snikers12368
Предмет: Алгебра,
автор: atakulovaguliza54
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: Karina3107