Предмет: Геометрия,
автор: funtimonia
помогите
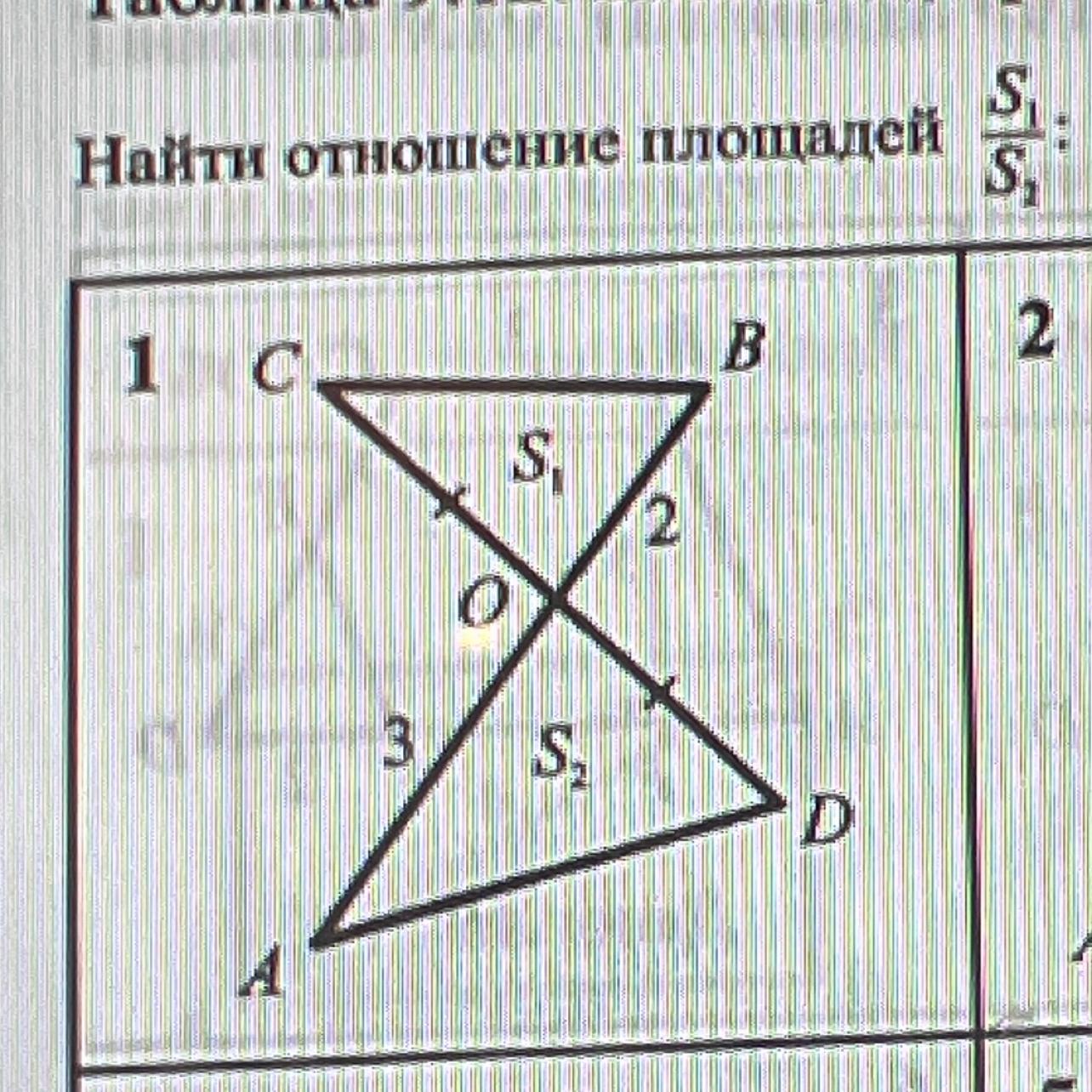
CO и OD пересекаются в точке О, CO=OD, AO=3, OB=2, найти отношение площадей
Приложения:
Ответы
Автор ответа:
0
Ответ: S1/S2=2/3
Объяснение:
Воспользуемся формулой площади треугольника
S=0.5*a*b*sinα
S1=0.5*CO*OB*sin∡COB =0.5*СО*2*sin∡COB= СО*sin∡COB (1)
S2=0.5*DO*AO*sin∡AOD (2)
Заметим, что ∡COB=∡AOD ( вертикальные) и CO=OD (по условию)
=> (2) перепишем так :
S2=0.5*CO*3*sin∡COB =1.5*CO*sin∡COB (2-1)
Разделим (1) на (2-1) :
S1/S2=СО*sin∡COB /( 1.5*CO*sin∡COB) = 1/1.5= 10/15=2/3
S1/S2=2/3
Похожие вопросы
Предмет: Информатика,
автор: mirizadegulsan
Предмет: География,
автор: illarion47
Предмет: Математика,
автор: akylajmedetova69
Предмет: Биология,
автор: ruslan15982
Предмет: Математика,
автор: ivanbushuev53