Предмет: Геометрия,
автор: piterbest888
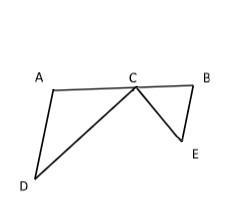
На рисунке AD || BE, AC = AD, BC = BE. Найдите угол DCE помогите пожалуйста
Приложения:
Ответы
Автор ответа:
3
т.к. по условию треугольники DАС и ЕВС равнобедренные, то их углы при основании равны. пусть ∠АDС=∠АСD=х, ∠BСE=∠BЕC=у, а т.к. сумма углов треугольника 180°, то ∠DАС=180°-2х, ∠ЕВС=180°-2у,
∠DАС+ ∠ЕВС=180°-2х+180°-2у=360°-2х-2у,
по свойству внутренних односторонних при параллельных АD и ВЕ и секущей АВ сумма углов ∠DАС+ ∠ЕВС=180°,
360°-2х-2у=180°⇒180°=2х+2у, х+у=90°, угол АСВ=180°, т.к. он
развернутый, искомый угол DCЕ=180°-(х+у)=180°-90°=90°
Ответ 90°
Похожие вопросы
Предмет: Музыка,
автор: lidorika
Предмет: Українська мова,
автор: arsenshaban1337
Предмет: Химия,
автор: melek2009v
Предмет: Математика,
автор: Аноним