Предмет: Алгебра,
автор: feyyyaa
,,,,,,,,,,,,,,,,,,,,,,
Приложения:
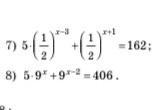
Ответы
Автор ответа:
1
Ответ:
7) -2; 8) 2
Объяснение:
Решить уравнения:
Свойства степеней:
feyyyaa:
спасибо большое!!!
Похожие вопросы
Предмет: Французский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: ajdanaasema74
Предмет: Математика,
автор: liangelina536
Предмет: Биология,
автор: akmal100708
Предмет: Литература,
автор: Аноним