Если ответ будет правильный дам корону Помогите пожалуйста
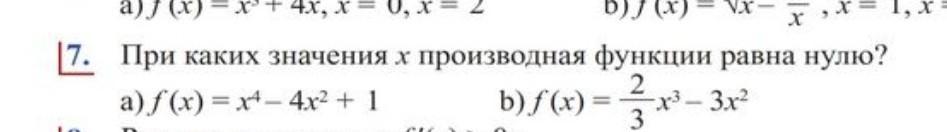
Ответы
Ответ:
Производная функции f(x)=x⁴-4x²+1 равна нулю при х₁=0, х₂=√2 либо х₃=(-√2).
Производная функции f(x) = 2/3x³-3x² равна нулю при х₁=0 и х₂=3.
Объяснение:
а) f(x) = x⁴-4x²+1
Находим производную функции, применяя (xⁿ)' = xⁿ⁻¹; (f(x)±g(x))' = f'(x)± g'(x) и (с)' = 0.
f'(x) = (x⁴-4x²+1)' = 4x⁴⁻¹-4*2x²⁻¹+0 = 4x³-8x
Приравниваем найденную производную f'(x)=4x³-8x к нулю и решаем уравнение.
4x³-8x = 0
4х(х²-2) = 0
4х = 0 х²-2=0
х = 0 х² = 2
х₁=0, х₂=√2, х₃=(-√2)
Производная функции f(x)=x⁴-4x²+1 равна нулю при х₁=0, х₂=√2 либо х₃=(-√2).
б) f(x) = 2/3x³-3x²
Находим производную функции, применяя те же правила дифференцирования, что и в первом варианте.
f'(x) = (2/3x³-3x²)' = 2/3*3x³⁻¹-3*2x²⁻¹ = 2x²-6x
Приравниваем найденную производную f'(x)=2x²-6x к нулю и решаем уравнение.
2x²-6x = 0
2x(x-3) = 0
2x = 0 x-3 = 0
x₁=0, x₂=3
Производная функции f(x) = 2/3x³-3x² равна нулю при х₁=0 и х₂=3.