Предмет: Алгебра,
автор: alisafiorini13
ПОМОГИТЕ! ТЕСТ!
Непрерывная случайна величина X задана функцией распределения
(Фото)
Найдите значение функции плотности распределения этой случайной величины в точке 2,5 .
1) 1
2) 0
3) 59
4) 2536
Приложения:
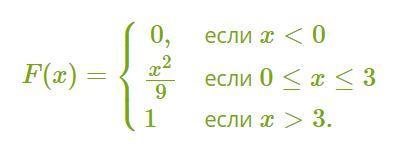
Ответы
Автор ответа:
2
Ответ: 5/9 .
Функция плотности - это производная от функции распределения :
Проверим, что функция f(x) действительно является функцией
плотности. Для этого проверим равенство:
.
Итак, функция f(x) действительно является функцией плотности .
Теперь найдём значение f(x) при х=2,5 .
Похожие вопросы
Предмет: Окружающий мир,
автор: katyauiioo
Предмет: Математика,
автор: tinamuradyan156
Предмет: Математика,
автор: mashalolstrahova
Предмет: Литература,
автор: Jkutf
Предмет: Українська мова,
автор: Mpfiif16