Предмет: Геометрия,
автор: piratonlain
В правильной четырёхугольной призме через диагональ основания проведено сечение параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2см, а её высота равна 4
Ответы
Автор ответа:
0
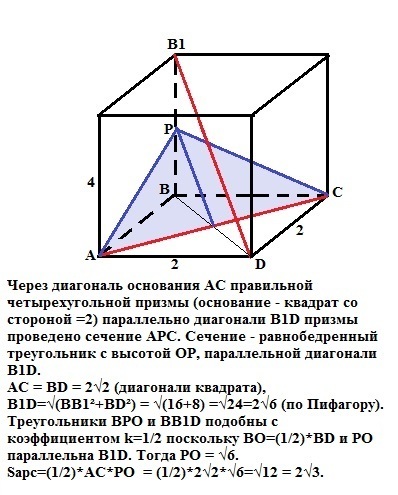
Через диагональ основания АС правильной четырехугольной призмы (основание - квадрат со стороной =2) параллельно диагонали B1D призмы проведено сечение АРС. Сечение - равнобедренный треугольник с высотой ОР, параллельной диагонали B1D. АС = BD = 2√2 (диагонали квадрата), B1D=√(BB1²+BD²) = √(16+8) =√24=2√6 (по Пифагору).
Треугольники ВРО и ВВ1D подобны с коэффициентом k=1/2 поскольку ВО=(1/2)*BD и РО параллельна B1D. Тогда РО = √6.
Sapc=(1/2)*AC*PO = (1/2)*2√2*√6=√12 = 2√3. Это ответ.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: soniacaluta
Предмет: Русский язык,
автор: karimmaier1979
Предмет: Химия,
автор: maksimklimik6
Предмет: История,
автор: Хафиза