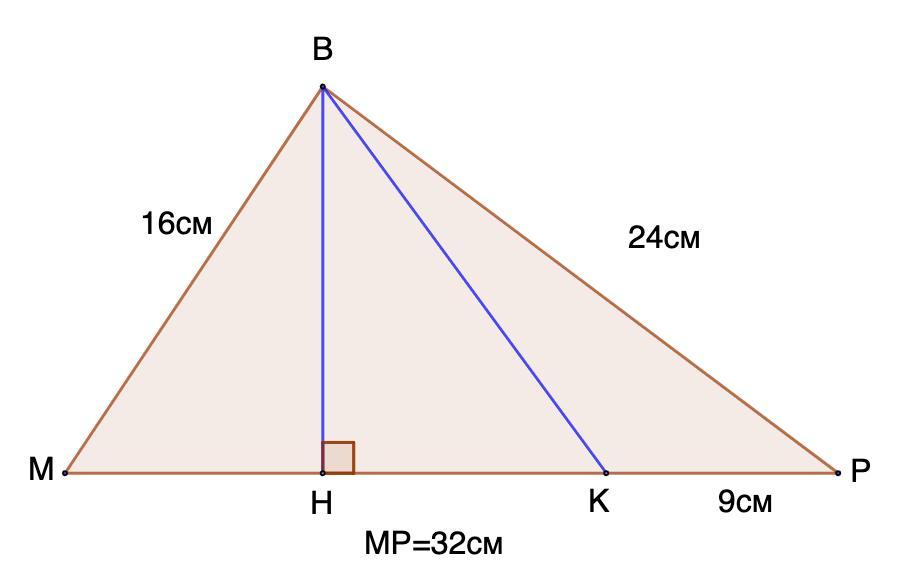
У трикутнику МВР відомо, що МВ = 16см, ВР = 24см, МР = 32см. На
стороні МР взято точку К, так що РК = 9см. Знайти відрізок ВК.
Ответы
Ответ:
Отрезок ВК равен 3√31 см.
Объяснение:
В треугольнике МВР известно, что МВ = 16 см, ВР = 24 см, МР = 32 см. На стороне МР взята точка К, так что РК = 9 см. Найти отрезок ВК.
Дано: ΔМВР;
МВ = 16 см, ВР = 24 см, МР = 32 см.
К ∈ МР; РК = 9 см.
Найти: ВК.
Решение:
Проведем высоту ВН.
1. Рассмотрим ΔМВР.
МВ = 16см, ВР = 24см, МР = 32см.
Найдем площадь по формуле Герона:
,
где р - полупериметр; a, b, c - стороны треугольника.
Р(ΔМВР) = 16 + 24 + 32 = 72 (см)
р = 72 : 2 = 36 (см)
Площадь треугольника равна 48√15 см².
С другой стороны, площадь можно найти по формуле:
где а - сторона треугольника, h - высота, проведенная к этой стороне.
S = 48√15 см², MP = 32 см.
Найдем высоту:
2. Рассмотрим ΔМВН - прямоугольный.
ВН = 3√15 см; МВ = 16 см.
По теореме Пифагора найдем МН:
МН² = МВ² - ВН² = 256 - 135 = 121 ⇒ МН = 11 (см)
3. Рассмотрим ΔНВК - прямоугольный.
НК = МР - КР - МН = 32 - 9 - 11 = 12 (см)
По теореме Пифагора найдем ВК:
ВК² = ВН² + НК² = 135 + 144 = 279; ВК = 3√31 (см)
Отрезок ВК равен 3√31 см.
#SPJ1