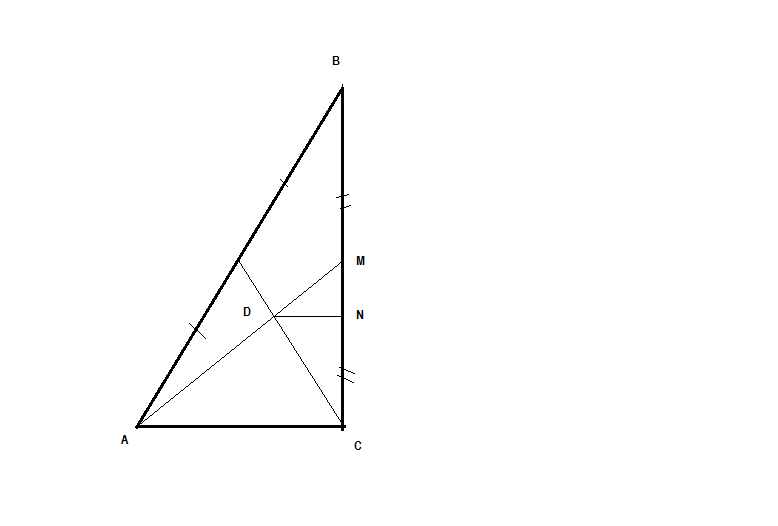решите Егэ С-4 только ерунду всякую не пишите
конус образован вращением прямоугольного треугольника площадью S вокруг одного из катетов. Найти объем конуса, еслт длина окружности , описанной при вращении этого треугольника точкой персечения его медиан, равна L РЕШЕНИЕ и РИСУНОК
Ответы
см. рисунок во вкладке
Объем конуса V=1/3*pi*r^2*h (1)
Пусть конус образован вращением треугольника АВС вокруг катета ВС,
тогда радиус основания АС=r ; высота BC=h.
По условию 1/2*rh=S подставим в (1)
V= (2pi/3*r) * (1/2*rh)=2pi/3*r*S. (2)
Кроме того , по условию , 2pi*DN=L , где D- точка пересечения медиан, a DN перпендикуляр к ВС.
Но DN : AC =DM : AM = 1:3 (на основании свойства медиан)
откуда DN=r/3 , следовательно L=2pi/3*r , отсюда r=3L/2pi. (3)
Подставим (3) в (2)
V=2pi/3*S*3L/2pi = SL
Ответ V=SL