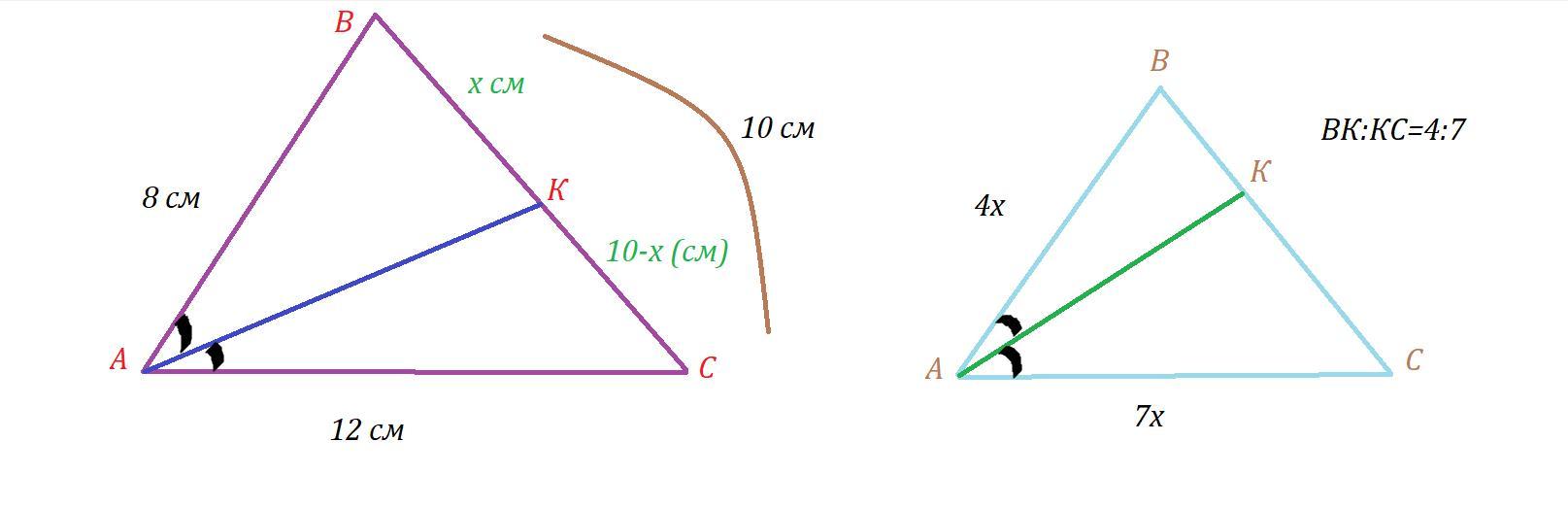
Відрізок AK – бісектриса трикутника ABC. Знайдіть:
1) відрізки BK і KC, якщо AB = 8 см, AC = 12 см, BC = 10 см;
2) сторони AB і AC, якщо AC – AB = 9 см, BK : KC = 4 : 7.
Ответы
Ответ: 4 см и 6см; 12 см и 21 см.
Объяснение:
Отрезок AK-биссектриса треугольника ABC. Найдите:
1) отрезки BK и KC, если AB = 8 см, AC = 12 см, BC = 10 см;
2) стороны AB и AC, если AC – AB = 9 см, BK : KC = 4 : 7.
1.
Дано: ΔАВС: АB = 8 см, AC = 12 см, BC = 10 см, АК - биссектриса
Найти: ВК, КС
Решение:
Пусть х - коэффициент пропорциональности, тогда ВК=х, а КС = 10-х
Используемое свойство: биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон ⇒ Составим и решим пропорцию:
12х = 8(10-х)
12х=80-8х
12х+8х=80
20х=80
х=80:20
х=4 (см) - сторона ВК, а сторона КС=10-х=10-4=6 (см)
проверим: ВС=ВК+КС=4+6=10 (см) - Верно.
Ответ: отрезки ВК и КС равны 4 см и 6 см.
2.
Дано: ΔАВС: AC – AB = 9 см, BK : KC = 4 : 7, АК - биссектриса
Найти: АВ, АС
Решение:
так как биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному
углу сторон, то , Пусть х - коэффициент пропорциональности, а так как ВК:КС=4:7, то из этого следует,
что . По условию AC – AB = 9 ⇒ Составим и решим
уравнение:
7х-4х=9
3х=9
х=3 (см) , подставим найденное значение в искомые стороны:
АВ=4х=4*3=12 (см) и АС=7х=7*3=21 (см)
проверим: АС - АВ = 9
21 - 12 = 9
9= 9 Сходится, значит решено верно.
Ответ: отрезки АВ и АС равны 12 см и 21 см.
#SPJ1