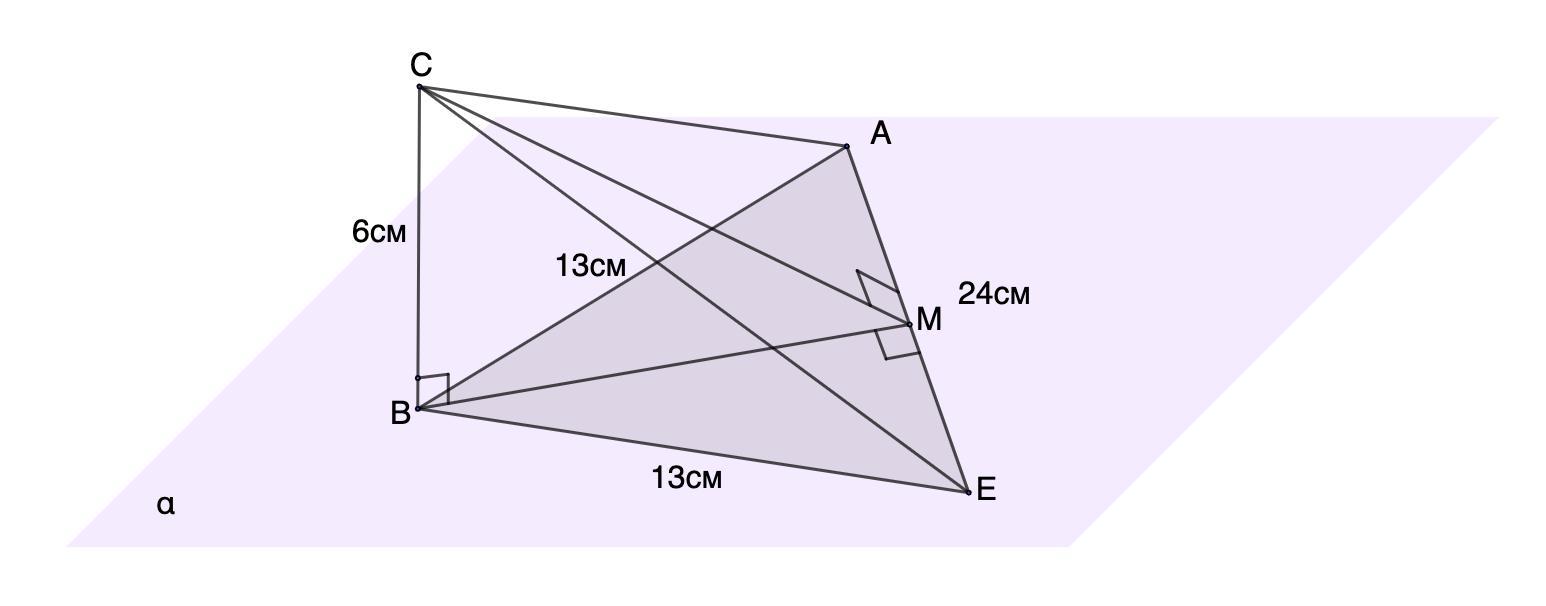
Рівнобедрений трикутник ABE знаходиться у площині α. Бічні сторони трикутника ABE дорівнюють 13 см, а сторона основи AE= 24 см. До цієї площини проведені перпендикуляр CB, який дорівнює 6 см, і похилі CA і CE. Обчисліть відстань від точки C до сторони трикутника AE.
Ответы
Ответ:
Расстояние от точки C до стороны треугольника AE равно √61 см.
Объяснение:
Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны 13 см, а сторона основания AE= 24 см. К этой плоскости проведены перпендикуляр CB, который равен 6 см, и наклонные CA и CE.Вычислите расстояние от точки C до стороны треугольника AE.
Дано: ΔАВЕ - равнобедренный;
ВЕ = ВА = 13 см; АЕ = 24 см.
СВ ⊥ АВЕ; СВ = 6 см;
СА и СЕ - наклонные;
Найти: расстояние от точки C до AE.
Решение:
В ΔАВЕ проведем высоту ВМ. Соединим В и С.
ВМ ⊥АЕ (построение)
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒СМ ⊥ АЕ
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ СМ - искомый отрезок.
1. Рассмотрим ΔЕВМ - прямоугольный.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ ЕМ = МА = 24 : 2 = 12 (см)
ВЕ = 13 см (условие)
По теореме Пифагора найдем ВМ:
ВМ² = ВЕ² - МЕ² = 169 - 144 = 25 ⇒ ВМ = √25 = 5 (см)
2. Рассмотрим ΔВСМ - прямоугольный.
По теореме Пифагора найдем СМ.
СМ² = ВМ² + ВС² = 25 + 36 = 61 ⇒ СМ = √61 см.
Расстояние от точки C до стороны треугольника AE равно √61 см.
#SPJ1