33.5. При каких значениях а многочлен P(x) имеет корень, равный 2:
2) P(x) = -x³ + x² - 2x + a² - a;
4) P(x) = x³ + 2x²- 5x + a² - 5a;
?? ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО
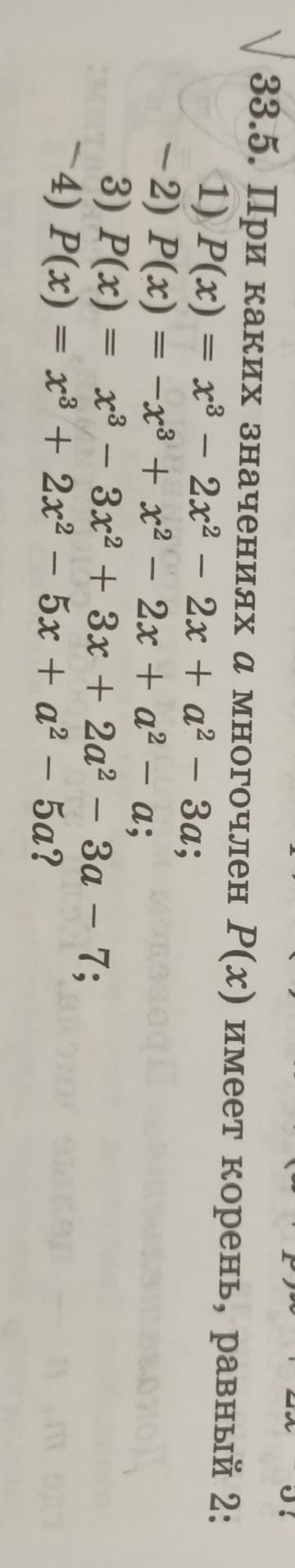
Ответы
Ответ:
1) a₁ = 4 , a₂ = -1
3) a₁ = - 1 , a₂ = 2,5
4) a₁ = 3 , a₂ = 2
Объяснение:
33.5. При каких значениях а многочлен P(x) имеет корень, равный 2:
1) P(x) = x³ - 2x² - 2x + a² - 3a
Т.к 2 , является корнем уравнения x³ - 2x² - 2x + a² - 3a = 0 , то при подстановке данный многочлен должен быть равен нулю
P(2) = 2³ - 2·2² - 2·2 + a² - 3a = 0
8 - 8 - 4 + a² - 3a = 0
a² - 3a - 4 = 0
2) P(x) = -x³ + x² - 2x + a² - a
P(2) = -(2³) + 2² - 2·2 + a² - a = 0
-8 + 4 - 4 + a² - a = 0
a² - a - 8 = 0
D = 1 + 32 = 33
3) P(x) = x³ -3x² + 3x + 2a² - 3a - 7
P(2) = 2³ - 3·2² + 3·2 + 2a² - 3a - 7 = 0
8 - 12 + 6 + 2a² - 3a - 7 = 0
2a² - 3a - 5 = 0
Если у квадратного уравнения
ax² + bx + c = 0
a - b + c = 0 ⇒ x₁ = - 1
Как раз в нашем случае :
2 - (-3 ) - 5 = 2 + 3 - 5 = 0
⇒ a₁ = - 1
А второй корень , мы можем найти по теореме Виета
ax² + bx + c = 0
4) P(x) = x³ + 2x²- 5x + a² - 5a
P(2) = 2³ + 2·2²- 5·2 + a² - 5a = 0
8 + 8 - 10 + a² - 5a = 0
a² - 5a + 6 = 0
#SPJ1