Предмет: Математика,
автор: ruskarandash
Вычислить пределы, применяя правило Лопиталя. (интересно решение)
Приложения:
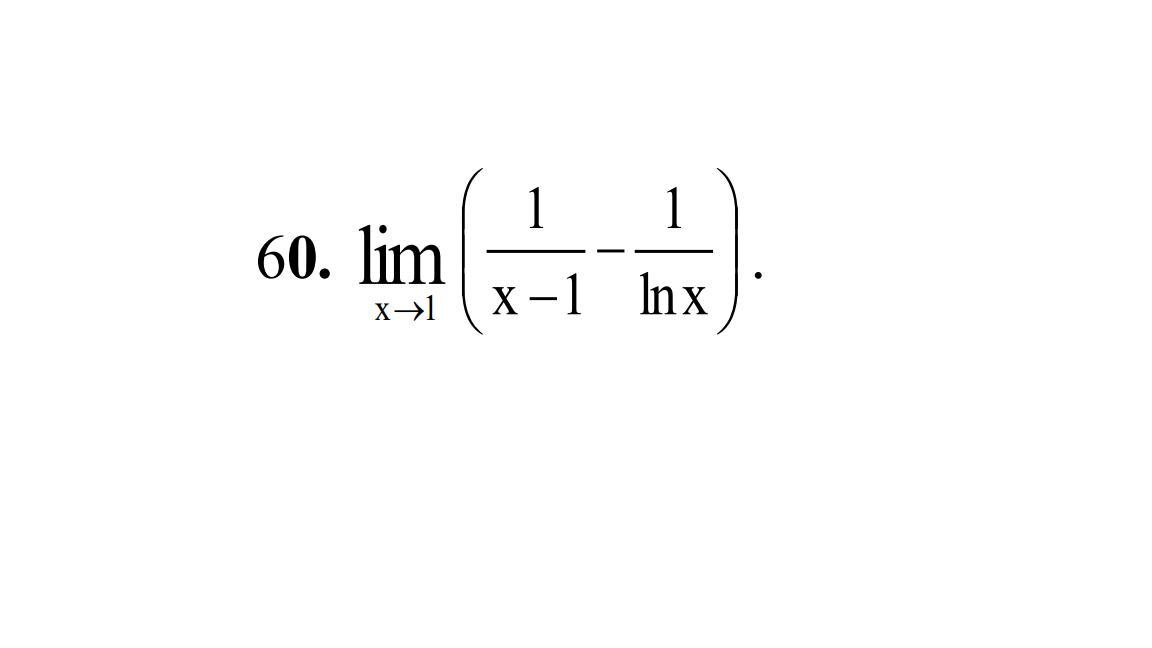
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Вычислить пределы, применяя правило Лопиталя.
- Правило Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞. Суть правила: предел отношения функций равен пределу отношения их производных.
Неопределенность 0/0.
Применим правило Лопиталя:
Опять получили неопределенность 0/0.
Применим еще раз правило Лопиталя:
Похожие вопросы
Предмет: Химия,
автор: nasstakrl
Предмет: Английский язык,
автор: diannelkaa
Предмет: Физика,
автор: lipa3420
Предмет: Химия,
автор: uchenik2776
Предмет: Физика,
автор: polinaturcin78