В группе из учеников 25 человек владеют китайским языком, 28-испанским,35-французким. Китайским и французким языками владеют 7 учеников, китайским и испанским- 9 учеников, испанским и французким-10 учеников. Всеми тремя языками владеют 3 человека. Сколько человек в группе?
Ответы
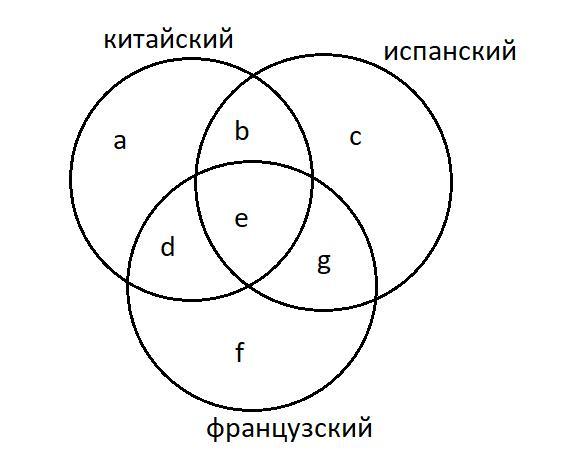
Данную задачу можно решить с помощью кругов Эйлера (на рисунке).
///////////////////////////////////////////////////////////////////////////////////
Описание областей:
a - только китайский;
b - только китайский и испанский;
c - только испанский;
d - только китайский и французский;
e - все языки;
f - только французский;
g - только французский и испанский;
///////////////////////////////////////////////////////////////////////////////////
Составим уравнения на основе условия задачи:
(для этого суммируем все области, где содержатся нужные языки)
a + b + d + e = 25
b + c + e + g = 28
d + e + f + g = 35
d + e = 7
b + e = 9
g + e = 10
e = 3
///////////////////////////////////////////////////////////////////////////////////
Найдём все переменные:
e = 3 (из условия)
g = 10 - 3 = 7
b = 9 - 3 = 6
d = 7 - 3 = 4
f = 35 - (d + e + g) = 35 - 14 = 21
c = 28 - (b + e + g) = 28 - 16 = 12
a = 25 - (b + d + e) = 25 - 13 = 12
///////////////////////////////////////////////////////////////////////////////////
Просуммируем все полученные области:
a + b + c + d + e + f + g = 12 + 6 + 12 + 4 + 3 + 21 + 7 = 65
///////////////////////////////////////////////////////////////////////////////////
Ответ: в группе 65 человек.