Question

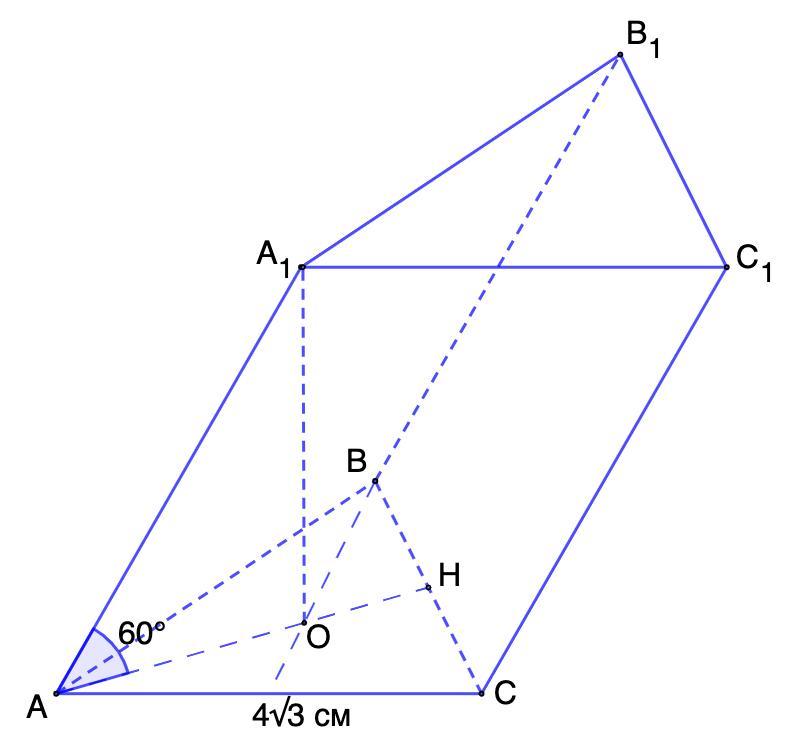
Основою похилої призми є правильний трикутник зі стороною 4√3см.Одна з вершин верхньої основи проектується в центр нижньої.Бічні ребра призми утворюють з площиною основи кут 60°.Знайдіть об'єм призми

Answer 1

Ответ:

Объем призмы равен 144 см³.

Объяснение:

Основой наклонной призмы является правильный треугольник со стороной 4√3 см. Одна из вершин верхнего основания проецируется в центр Нижнего. Боковые ребра призмы образуют с плоскостью основания угол 60°. Найдите объем призмы.

Дано: АВСА₁В₁С₁ - наклонная призма;

АВС - правильный треугольник; АС = 4√4 см;

А₁О ⊥ АВС; О - центр ΔАВС;

∠А₁АН = 60⁰.

Найти: V - объем призмы.

Решение:

Объем призмы найдем по формуле:

V = Sосн. · H ,

где Sосн. - площадь основания; Н - высота призмы.

Площадь равностороннего треугольника:

$\displaystyle \bf \boxed { S=\frac{a^2\sqrt{3} }{4} }$

$\displaystyle S_{OCH.}=\frac{16\cdot 3\sqrt{3} }{4} =12\sqrt{3}\;_{(CM^2)}$

Площадь основания равна 12√3 см².

Найдем высоту.

О - центр ΔАВС.

• Центр равностороннего треугольника - точка пересечения медиан, высот, биссектрис.

Рассмотрим ΔАНС - прямоугольный.

АС = 4√3 см; СН = АС : 2 = 2√3 см (АН - медиана).

По теореме Пифагора найдем АН:

АН² = АС² - СН² = 16 · 3 - 4 · 3 = 36   ⇒   АН = √36 = 6 (см)

• Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, начиная от вершины.

⇒ АО = 6 · 2/3 = 4 (см)

Рассмотрим ΔАА₁О - прямоугольный.

∠А₁АН = 60⁰

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\;60^0=\frac{A_1O}{AO}\\ \\A_1O=AO \cdot tg\;60^0\\\\A_1O=4\cdot \sqrt{3}$

Высота призмы равна 4√3 см.

Можем найти объем:

V = 12√3 · 4√3 = 144 (см³)

Объем призмы равен 144 см³.

#SPJ1