Предмет: Математика,
автор: Ava9141
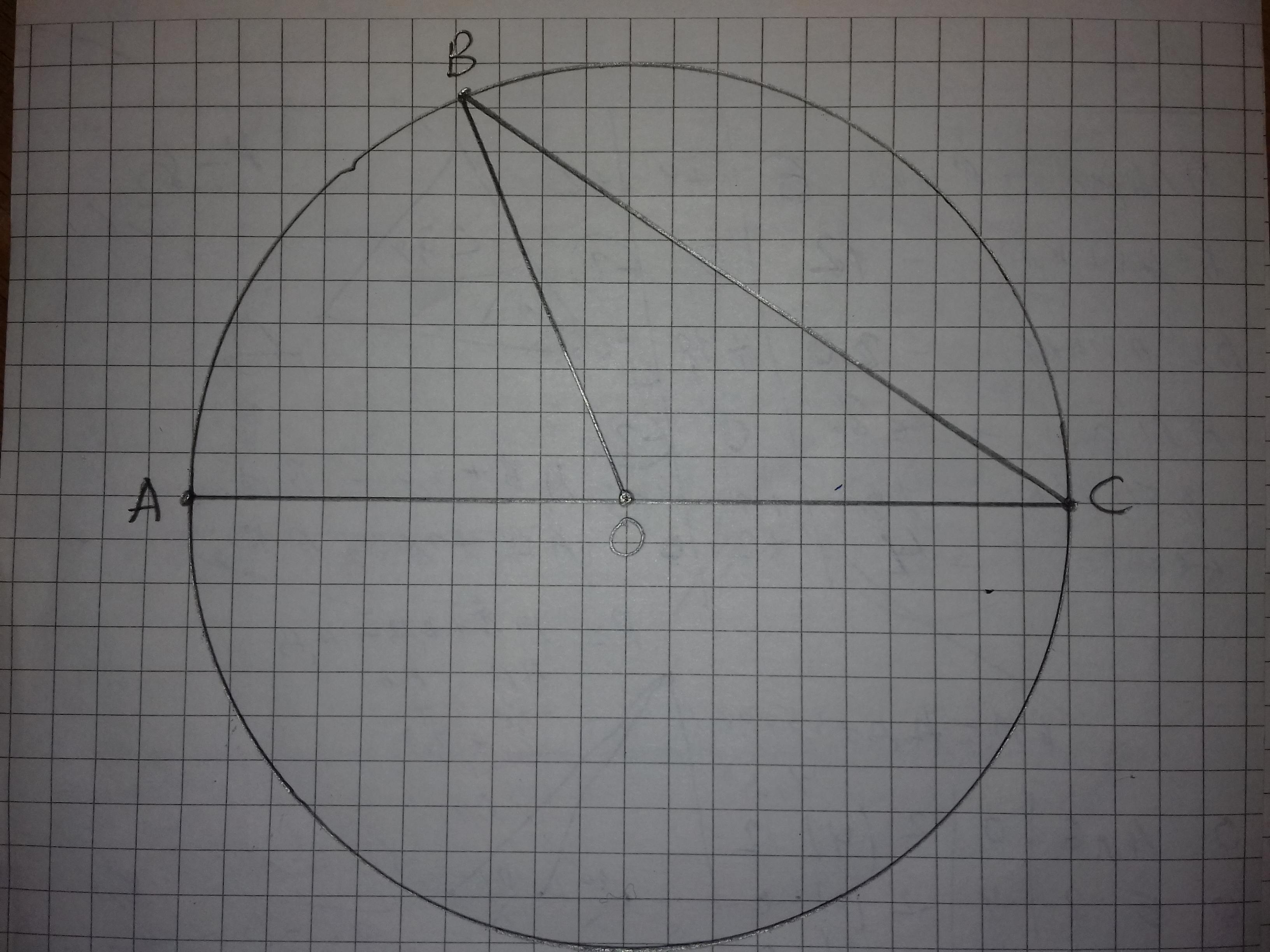
Точки A, B и C лежат на окружности, причём AC - диаметр окружности. Градусная мера дуги BC равна 114 градусов. Найдите градусную меру угла BCA.
Ответы
Автор ответа:
1
Відповідь:
∠ВСА = 33°.
Покрокове пояснення:
Точка О - центр окружности и середина отрезка АС ( так как АС - диаметр окружности ).
Рассмотрим треугольник ОВС. Он равнобедренный ( так как точки В и С лежат на окружности ) ОВ = ОС = Rокр. и как следствие ∠ОВС = ∠ОСВ.
Так как градусная мера дуги BC равна 114°, то и ∠ВОС = 114°
Поскольку сумма углов треугольника равна 180°, то:
∠ОВС = ∠ОСВ = ( 180° - ∠ВОС ) / 2 = ( 180° - 114° ) / 2 = 66° / 2 = 33°.
∠ВСА = ∠ОВС = 33°.
Приложения:
Ava9141:
Спасибо)
Похожие вопросы
Предмет: География,
автор: mixiqws
Предмет: Геометрия,
автор: ajfjr
Предмет: Қазақ тiлi,
автор: maksik9526
Предмет: Қазақ тiлi,
автор: kamaevdan621
Предмет: История,
автор: unik20000