Помогите пожалуйста с дискерной математикой

Ответы
Відповідь:
Пояснення:
якщо х належить до множини N={1,2,3,4,5}
якщо у належить до множини N={1,2,3,4,5}
то не для всіх пар <x,y> справедливо що 3x+у належить до множини N={1;2;3;4;5}
можем виділити тільки <1;1> та <1;2>
саме вони утворюють відношення p і ніякі інші
тому що
для пари <1;1> 3x+у = 3*1+1=4 ∈ N={1;2;3;4;5}
для пари <1;2> 3x+2 = 3*1+2=5 ∈ N={1;2;3;4;5}
для будь якої іншої пари це не виконується
наприклад
для пари <2;1> 3x+2 = 3*2+1=7 ∉ N={1,2,3,4,5}
p={<1;1> ; <1;2>} - відношення p складається з двох елементів
властивості відношення р
1) рефлексивність - ні
бо в відношення p не входять всі пари накшталт <1;1> <2;2> <3;3> <4;4> <5;5>
2) антирефлексивність - ні
бо в відношення p входить пара <1;1> з однакових елементів
3) симметричніснть - ні
бо в відношення p входить пара <1;2> але не входить симметрична їй пара <2;1>
4) антисимметричніснть - ні
бо в відношення p входить пара <1;1> що симметрична сама собі
5) транзитивніснть - так
х належить до множини N={1,2,3,4,5}
у належить до множини N={1,2,3,4,5}
z належить до множини N={1,2,3,4,5}
відношення p між х; у складається з пар
х=1; у=1
х=1; у=2
відношення p між y; z складається з пар
y=1; z=1
y=1; z=2
відношення p між x; z складається з пар
x=1; z=1
x=1; z=2
для всіх таких елементів х у z що одночасно входять в відношення p{<x;y>} та p{<y;z>} обов'язково утворюють відношення p{<x;z>}
6) зв'язність - ні
пояснювати не буду бо в запитання не входить і я втомився
*********************************************************************************************
г угл переклад
если х относится к множеству N={1,2,3,4,5}
если у относится к множеству N={1,2,3,4,5}
то не для всех пар <x,y> справедливо что 3x+у относится к множеству N={1;2;3;4;5}
можем выделить только <1;1> и <1;2>
именно они образуют отношение p и никакие другие
потому что
для пары <1;1> 3x+у = 3*1+1=4 ∈ N={1;2;3;4;5}
для пары <1;2> 3x+2 = 3*1+2=5 ∈ N={1;2;3;4;5}
для любой другой пары это не выполняется
к примеру
для пары <2;1> 3x+2 = 3*2+1=7 ∉ N={1,2,3,4,5}
p={<1;1>; <1;2>} – отношение p состоит из двух элементов
свойства отношения р
1) рефлексивность – нет
ибо в отношение p не входят все пары вроде <1;1><2;2><3;3><4;4><5;5>
2) антирефлексивность – нет
ибо в отношение p входит пара <1;1> из одинаковых элементов
3) симметричность – нет
ибо в отношение p входит пар <1;2> но не входит симметричная ему пара <2;1>
4) антисимметричность – нет
ибо в отношение p входит пара <1;1> что симметрична сама себе
5) транзитивность - да
х относится к множеству N={1,2,3,4,5}
у относится к множеству N={1,2,3,4,5}
z относится к множеству N={1,2,3,4,5}
отношение p между х; в состоит из пар
х=1; у=1
х=1; у=2
отношение p между y; z состоит из пар
y=1; z=1
y=1; z=2
отношение p между x; z состоит из пар
x=1; z=1
x=1; z=2
для всех таких элементов х у z одновременно входящих в отношение p{<x;y>} и p{<y;z>} обязательно образуют отношение p{<x;z>}
6) связность – нет
объяснять не буду потому что в вопрос не входит и я устал
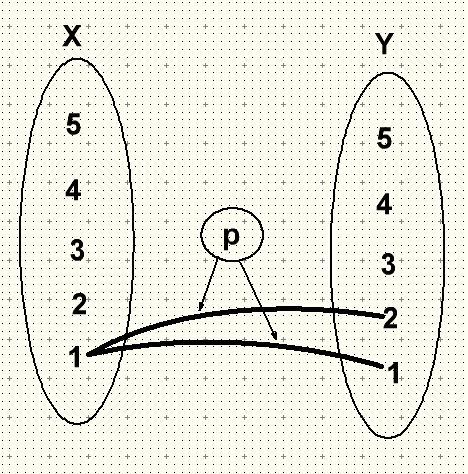
це те, як я зрозумів умову
1) я не пишу дано. мои решения в строчку или картинка с редактора формул
2) я помогаю тем кто помогает другим.
перед тем как отвечать я смотрю ответы тех кому отвечаю.
когда поможете кому-либо и если писать с дано не обязательно - дайте знать.
5 минут назад открыл в инете определения и могу по ним ответить
без рисования
вы хотите чтобы незнаток типа меня ответил вам на этот вопрос ?
гарантию что 100% верно дать не могу