Предмет: Геометрия,
автор: 160777
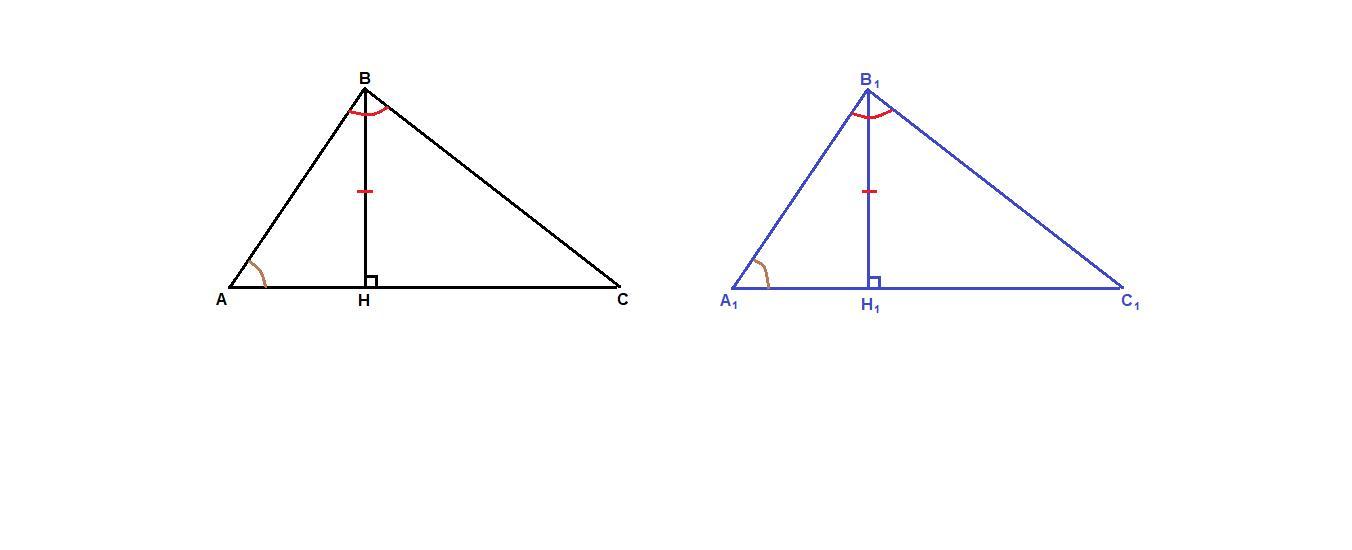
Докажите, что треуг.АВС = треуг. А1В1С1, если уголА = угол А1, угол В = угол В1, и ВН = В1Н1, где ВН и В1Н1 - высоты треугольников АВС и А1В1С1.
Ответы
Автор ответа:
0
ВН = В₁Н₁ по условию,
∠А = ∠А₁ по условию,
∠АНВ = ∠А₁Н₁В₁ = 90°, так как ВН и В₁Н₁ высоты, ⇒
ΔАВН = ΔА₁В₁Н₁ по катету и противолежащему острому углу.
Значит, АВ = А₁В₁.
Тогда ΔАВС = ΔА₁В₁С₁ по стороне и двум прилежащим к ней углам:
АВ = А₁В₁ (доказано выше),
∠А = ∠А₁ и ∠В = ∠В₁ по условию.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ainagulbakmanova
Предмет: Қазақ тiлi,
автор: indirakendebaj
Предмет: Физика,
автор: ktahmina62585
Предмет: Химия,
автор: laura96