Предмет: Алгебра,
автор: fantabs988
розв'яжіть систему рівнянь. будь ласка
Приложения:
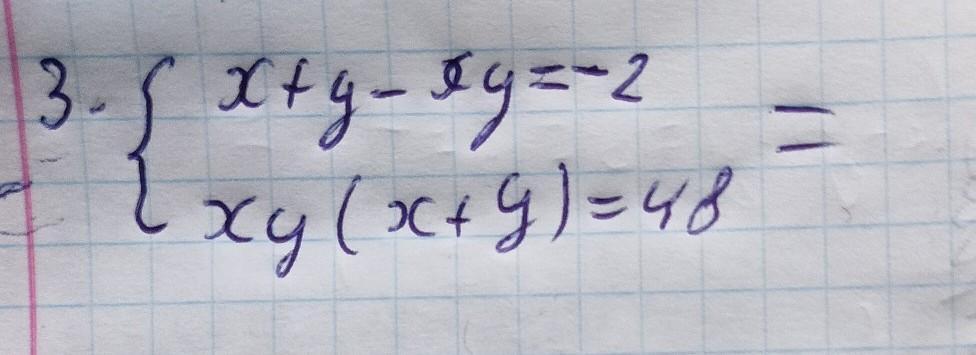
Ответы
Автор ответа:
0
Відповідь:
Пояснення:
3 . Зробити заміну : x + y = u ; xy = v , а далі рішати простішу систему підстановкою . Потім повернутися до старих змінних .
# Може пропущено якийсь знак , бо виходять складні вирази .
Автор ответа:
1
Объяснение:
Пусть х+у=t, xy=v ⇒
Похожие вопросы
Предмет: Алгебра,
автор: 2356533
Предмет: Українська мова,
автор: katerina2011katerina
Предмет: Українська мова,
автор: golomidovanasta5
Предмет: Английский язык,
автор: spoodeege
Предмет: Математика,
автор: Аноним