Предмет: Геометрия,
автор: VaytV
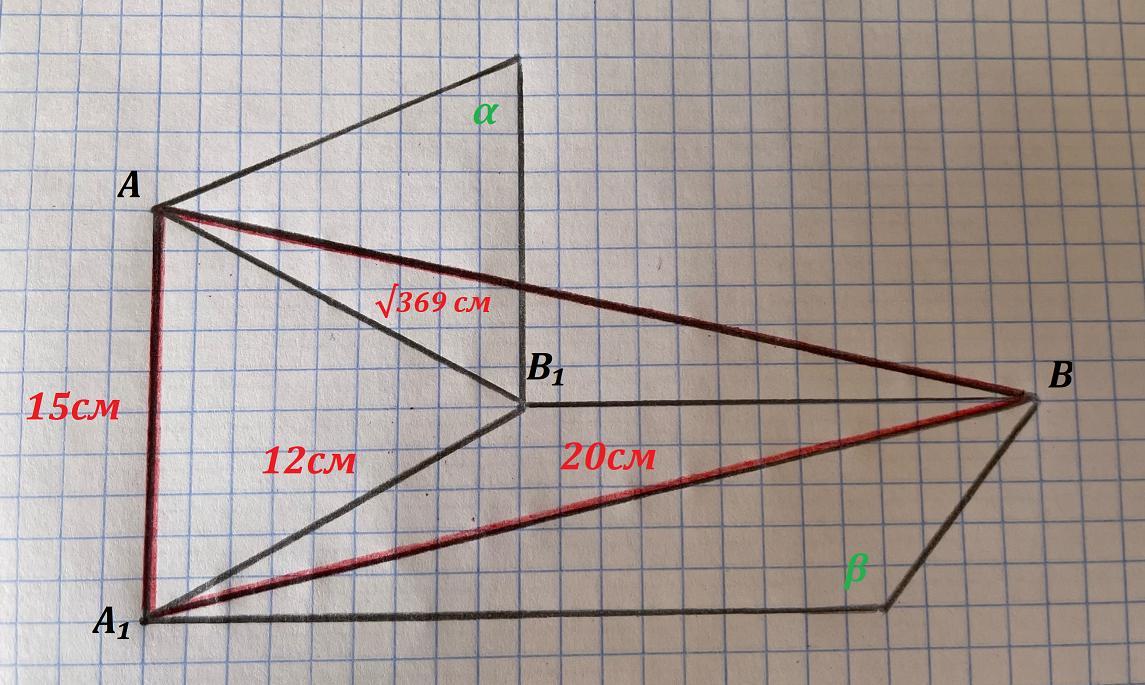
Кінці відрізка лежать у двох взаємно перпендикулярних площинах. Проекції відрізка на кожну із площин дорівнюють √369см і 20 см відповідно. Відстань між основами перпендикулярів, проведених із кінців відрізка до площин, дорівнює 12 см. Знайдіть довжину даного відрізка.
Ответы
Автор ответа:
8
Ответ: длина отрезка АВ равна 25 см
Объяснение:
Концы отрезка лежат в двух взаимно перпендикулярных плоскостях. Проекции отрезка на каждую из плоскостей равны √369см и 20см соответственно. Расстояние между основаниями перпендикуляров, проведенных из концов отрезка к плоскостям, равно 12 см. Найдите длину данного отрезка.
Дано:
АА₁ ⊥ β
А₁В проекция АВ на β
ВВ₁ ⊥ α
АВ₁ проекция на α
Найти: АВ
Решение:
1) ΔАА₁В₁ : ∠А₁ = 90°, по т. Пифагора найдем длину стороны АА₁
⇒
⇒
(см)
2) ΔАА₁В : ∠А₁ = 90°, по т. Пифагора найдём искомую сторону АВ:
Примечание: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов
⇒
⇒
(см)
#SPJ1
Приложения:
Nangw:
Спасибо!
Похожие вопросы
Предмет: Окружающий мир,
автор: yznavay111
Предмет: Математика,
автор: martacernuh
Предмет: История,
автор: vereskitti6
Предмет: История,
автор: Аноним
Предмет: Обществознание,
автор: mariannaburnaceva