549. Используя рисунок 63, найдите sin a, cos a, tg a u ctg a угла а, равного:
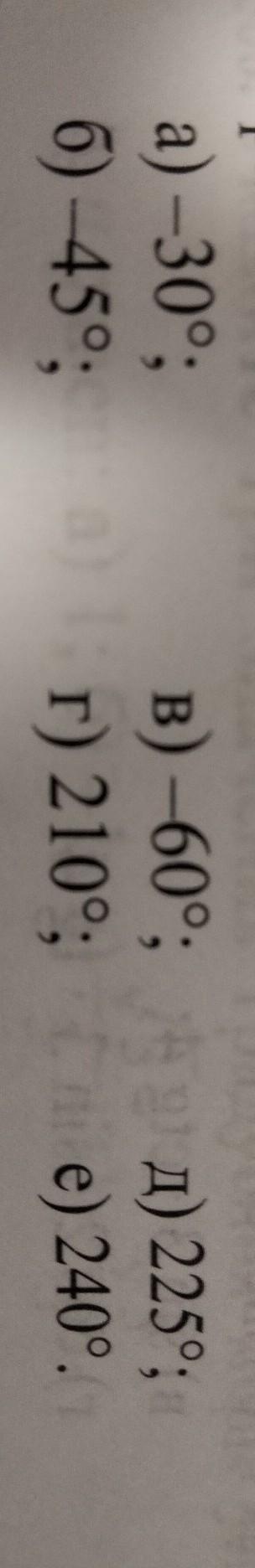
Ответы
Ответ:
Объяснение:
Нужно знать:
1) у = cosx - четная функция; y = sinx, y = tgx, y = ctgx - нечетные,
значит, cos(-α) = cosα, sin(-α) = -sinα, tg(-α) = -tgα, ctg(-α) = -ctgα;
2) значения тригонометрических функций углов 30°, 45° и 60°:
sin30° = cos60° = 1/2, cos30° = sin60° = √3/2, sin45° = cos45° = √2/2,
tg30° = ctg60° = 1/√3, tg60° = ctg30° = √3;
3) формулы приведения: sin(180° + α) = -sinα, cos(180° + α) = -cosα,
tg(180° + α) = tgα, ctg(180° + α) = ctgα.
Поэтому:
а) -30°
sin(-30°) = -sin30° = -1/2;
cos(-30°) = cos30° = √3/2;
tg(-30°) = -tg30° = -1/√3;
ctg(-30°) = -ctg30° = -√3;
б) -45°
sin(-45°) = -sin45° = -√2/2;
cos(-45°) = cos45° = √2/2;
tg(-45°) = -tg45° = -1;
ctg(-45°) = -ctg45° = -1;
в) -60°
sin(-60°) = -sin60° = -√3/2;
cos(-60°) = cos60° = 1/2;
tg(-60°) = -tg60° = -√3;
ctg(-60°) = -ctg60° = -1/√3;
г) 210°
sin(210°) = sin(180° + 30°) = -sin30° = -1/2;
cos(210°) = cos(180° + 30°) = -cos30° = -√3/2;
tg(210°) = tg(180° + 30°) = tg30° = 1/√3;
ctg(210°) = ctg(180° + 30°) = ctg30° = √3;
д) 225°
sin(225°) = sin(180° + 45°) = -sin45° = -√2/2;
cos(225°) = cos(180° + 45°) = -cos45° = -√2/2;
tg(225°) = tg(180° + 45°) = tg45° = 1;
ctg(225°) = ctg(180° + 45°) = ctg45° = 1;
е) 240°
sin(240°) = sin(180° + 60°) = -sin60° = -√3/2;
cos(240°) = cos(180° + 60°) = -cos60° = -1/2;
tg(240°) = tg(180° + 60°) = tg60° = √3;
ctg(240°) = ctg(180° + 60°) = ctg60° = 1/√3.
#SPJ1