Предмет: Геометрия,
автор: polinabobrova08
На сторонах AB и BC треугольника ABC лежат соответственно точки E и F так, что EF/AC = BE/BC = BF/AB. Чему равен угол EFC, если угол BAC=30?
Приложения:
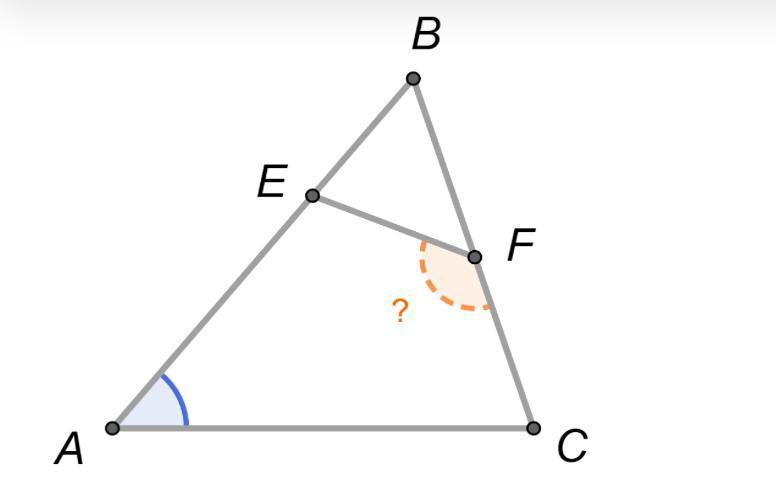
Ответы
Автор ответа:
2
Ответ:
Угол EFC равен 150°.
Объяснение:
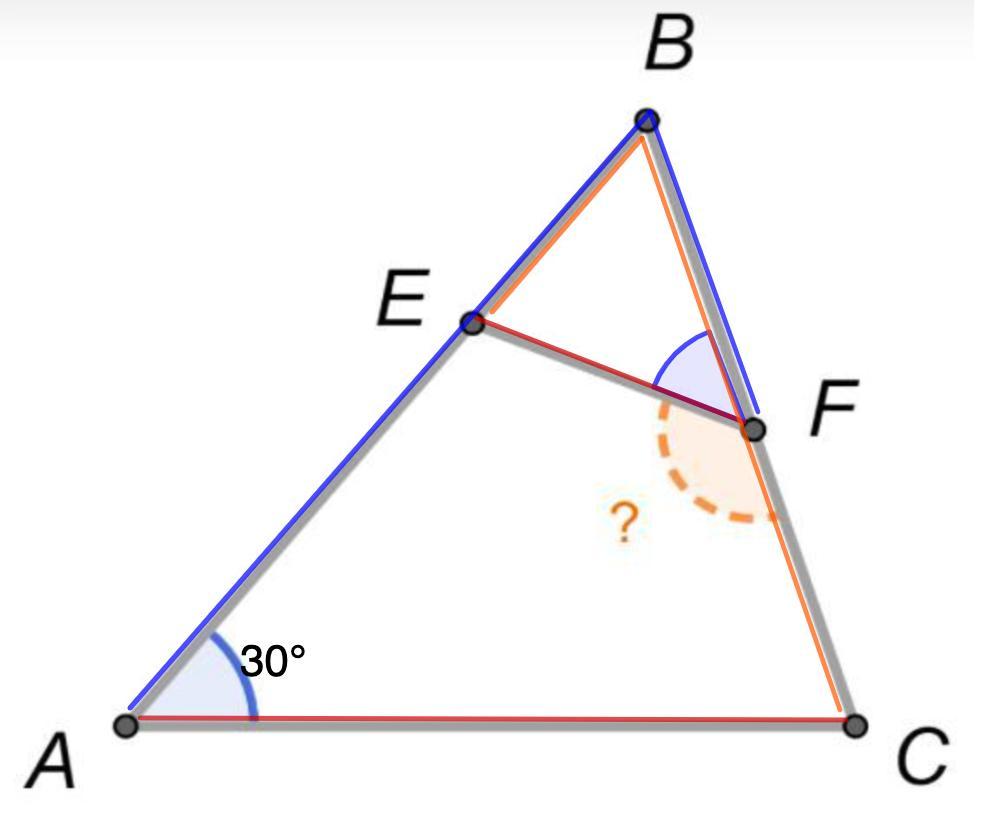
На сторонах AB и BC треугольника ABC лежат соответственно точки E и F так, что EF/AC = BE/BC = BF/AB. Чему равен угол EFC, если угол BAC=30?
Дано: ΔАВС;
E ∈ AB; F ∈ BC;
EF/AC = BE/BC = BF/AB.
∠BAC = 30°.
Найти: ∠EFC.
Решение:
Рассмотрим ΔАВС и ΔFBE.
EF/AC = BE/BC = BF/AB (условие)
- Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
⇒ ΔАВС ~ ΔFBE (по третьему признаку)
- В подобных треугольниках против сходственных сторон лежат равные углы.
⇒ ∠ВАС = ∠BFE = 30°
- Сумма смежных углов равна 180°.
⇒ ∠EFC = 180° - ∠BFE = 180° - 30° = 150°
Угол EFC равен 150°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: hcfgcvh
Предмет: Математика,
автор: nikabondar2909
Предмет: Геометрия,
автор: anasamarceva9
Предмет: Другие предметы,
автор: dbbss
Предмет: Информатика,
автор: kolamalyshev914