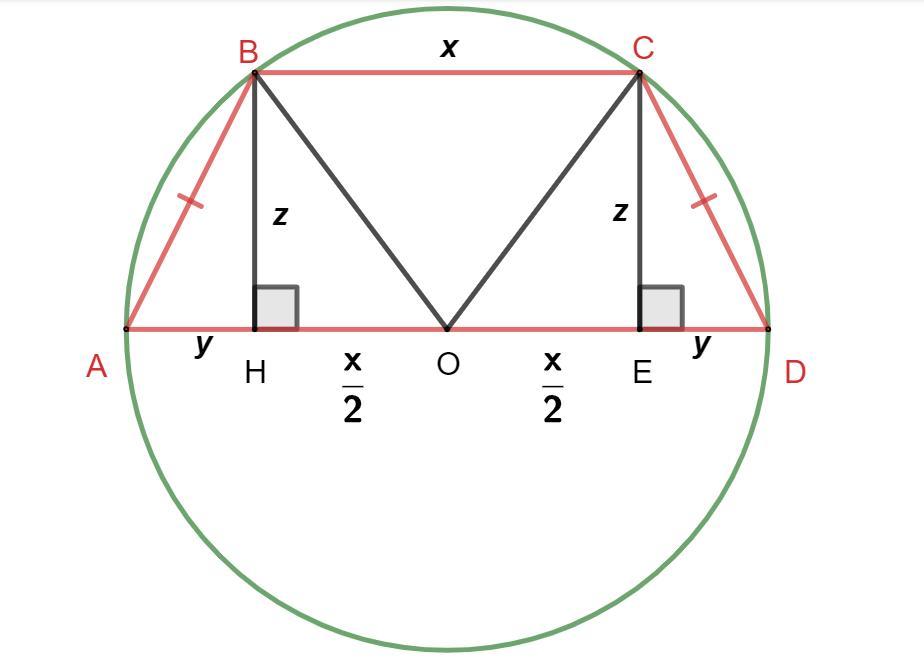
Найдите площадь трапеции ABCD, вписанной в окружность, если ее большее основание является диаметром ВН перпендикулярно AD, а отрезки АН и HD равны соответственно 4 см и 16 см.
Ответы
Ответ: Площадь трапеции ABCD равна 128 (см)²
Объяснение:
Выясняем , что из себя представляет данная трапеция
Если четырехугольник можно вписать в окружность , то сумма его противоположных углов будет равна 180°
* ∠A + ∠C = ∠B + ∠D = 180°
К тому же данный четырехугольник является трапецией , и поэтому сумма углов прилежащих к одной стороне трапеции также равна 180°
** ∠A + ∠B = ∠C + ∠D = 180°
Поскольку ∠A + ∠B = 180° , то ∠A = 180° - ∠B
Подставим в *
∠A + ∠C = 180°
180° - ∠B + ∠C = 180°
∠C - ∠B = 0
∠C = ∠B
Таким образом :
∠A + ∠C = ∠B + ∠D
∠A + ∠B = ∠B + ∠D
∠A = ∠D
Напрашивается логичный вывод , что если около трапеции , можно описать окружность , то она будет равнобедренной*
Находим неизвестное основание ( BC = x)
AD = AH + HD = x + 2y = 4 + 16 = 20 см
Радиус равен половине диаметра AB/2 = 20/2 = 10 см
Нам известно что AH = y = 4 см
x + 2y = 20
x + 4·2 = 20
BC = x = 12 см
Мы нашли величины оснований трапеций , теперь чтобы найти ее площадь , нужно найти величину ее высоты
Находим высоту трапеции (BH = z)
Проводим из центра окружности радиусы BO и OC , которые равны 10 см
Соответственно , проведя вторую высоту CE , легко заметить , что центр окружности O , разбивает отрезок HE = x = 12 см на два отрезка , которые равны между собой OH = OE = x/2 = 6 см , а равны потому что , очевидно что ΔABO равен ΔDCO , за счет того что к ним обоим проведены равные высоты (BH,CE) , и эти высоты будут отсекать равные отрезки AH = ED , OH = OE
Рассмотрим прямоугольный ΔBHO , легко заметить , что к нему применима теорема Пифагора
Находим площадь трапеции
Ее можно вычислить по формуле
где a,b - основания трапеции , а h - высота
#SPJ1