Предмет: Математика,
автор: Tadeush890
Объясните пожалуйста почему (х^2 + 4/х^2) стало (х - 2/х)^2 + 4
Приложения:
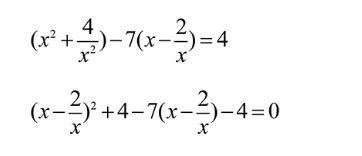
Ответы
Автор ответа:
1
Автор решения выделил полный квадрат, считая это действие очевидным.
Поясню, что произошло: — это почти квадрат разности, не хватает только удвоенного произведения (формула квадрата разности:
). У нас есть
— это
— и
— это
. Тогда
. Чтобы получить выражение
из
, необходимо отнять
, но поскольку этого
в уравнении не было, его нужно вернуть, то есть прибавить обратно. Вот и получаем, что
. Первые три слагаемых в правой части как раз и представляют квадрат разности, то есть
. Теперь подставляем
:
.
То, что мы сделали, называется выделением полного квадрата. Так автор и получил такой переход.
Похожие вопросы
Предмет: Физика,
автор: caramqbtw
Предмет: Русский язык,
автор: svetanorina2606
Предмет: Математика,
автор: elgrishenko756
Предмет: Геометрия,
автор: Hhhhhhhhre