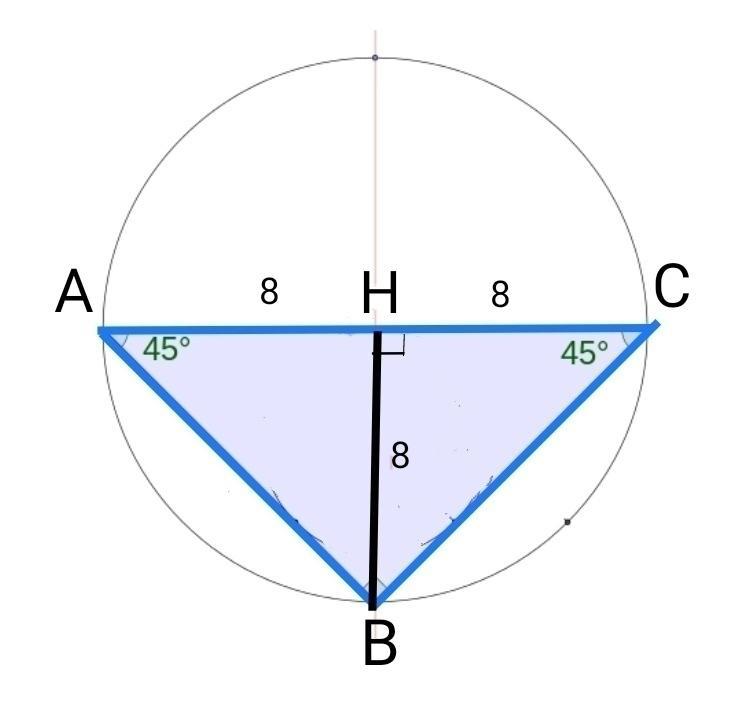
Знайдіть радіус кола описаного навколо рівнобедреного трикутника, основа якого дорівнює 16 см, а висота, проведена до основи, дорівнює 8 см.
Ответы
Ответ:
8 см
Объяснение:
Первый способ решения:
1. Рассмотрим равнобедренный треугольник АВС с основанием АС = 16 см и высотой ВН, проведённой к этому основанию, ВН = 8 см
По теореме ВН является медианой, тогда АН = НС = 16:2 = 8 (см).
2. Получили, что
АН = НС = ВР = 8 см, ∆ АВН прямоугольный равнобедренный, ∠ НАВ = ∠ НВА = 45°,
Аналогично и ∆ СВН прямоугольный равнобедренный, ∠ НСВ = ∠ НВС = 45°,
∠ АВС = 45° + 45° = 90°.
3. Центром окружности, описанной около прямоугольного треугольника АВС с прямым углом В, является по теореме середина гипотенузы АС точка Н, тогда
НА = R = 8 (см)
Второй способ решени:
1. Рассмотрим равнобедренный треугольник АВС с основанием АС = 16 см и высотой ВН, проведённой к этому основанию, ВН = 8 см
По теореме ВН является медианой, тогда АН = НС = 16:2 = 8 (см).
2. В ∆ АНВ по теореме Пифагора АВ = √(8²+8²) = 8√2 (см).
3. По теореме в любом треугольнике радиус описанной окружности может быть найден по формуле:
R = (abc)/(4S), где а, b, c - до ны сторон, а S - площадь треугольника.
В нашем случае
S = 1/2 • AC • BH = 1/2 • 16 • 8 = 64 (см²)
R = (16•8√2•8√2)/(4•64) = (16•2)/4 = 8 (см).
Третий способ решения:
Можно воспользоваться формулой
R = a/(2•sinA), где а - длина стороны треугольника, а sinA - это синус угла, противолежащего в треугольнике этой стороне.
В нашем случае
R = AB /(2•sinC) = 8√2/(2•√2/2) = 8√2/√2 = 8 (см).