Предмет: Геометрия,
автор: ilikegemsgensgems
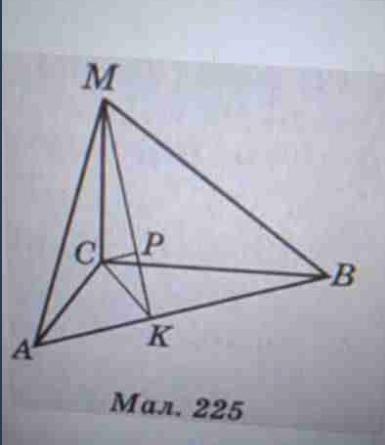
Даю 25 балів!! Якщо не здам сьогодні,мені будет погано.Через вершину прямого кута С ДАВС проведено перпенди- куляр СМ до площини трикутника (мал. 225). AC = 6, BC 8 см, СМ = 6,4 см. Знайдіть відстань: а) від точки М = до прямої АВ; б) від точки С до площини (АМВ).
Приложения:
zmeura1204:
Де мал.225?
Напишите что-нибудь, я не могу найти ваше задание в приложении.
Ответы
Автор ответа:
0
Ответ:
а) відстань від точки М до прямої АВ дорівнює 8см
б) відстань від точки С до площини (АМВ) дорівнює 3,84см
Объяснение:
∆АСВ- прямокутний трикутник, за умови ∠С=90°
За теоремою Піфагора:
АВ=√(АС²+СВ²)=√(6²+8²)=10см
СК- висота проведена до гіпотенузи.
СК=АС*СВ/2=6*8/10=4,8см.
СК перпендикулярно АВ, тоді МК перпендикулярно АВ, за теоремою о трьох перпендикулярах.
∆МСК- прямокутний трикутник.
За теоремою Піфагора:
МК=√(МС²+СК²)=√(6,4²+4,8²)=√(40,96+23,04)=
=√64=8см
_________________
б)
СР- висота трикутника ∆МСК, проведена до гіпотенузи МК
СР=МС*СК/МК=6,4*4,8/8=3,84см це і є відстань від точки С до площини (АМВ).
Похожие вопросы
Предмет: Химия,
автор: dima500592sss
Предмет: Английский язык,
автор: nasimzonvoh
Предмет: Алгебра,
автор: akundukpaev96
Предмет: Алгебра,
автор: gazuevahajbat
Предмет: Математика,
автор: denispsenicnuk