Предмет: Геометрия,
автор: vladislavkulyavets
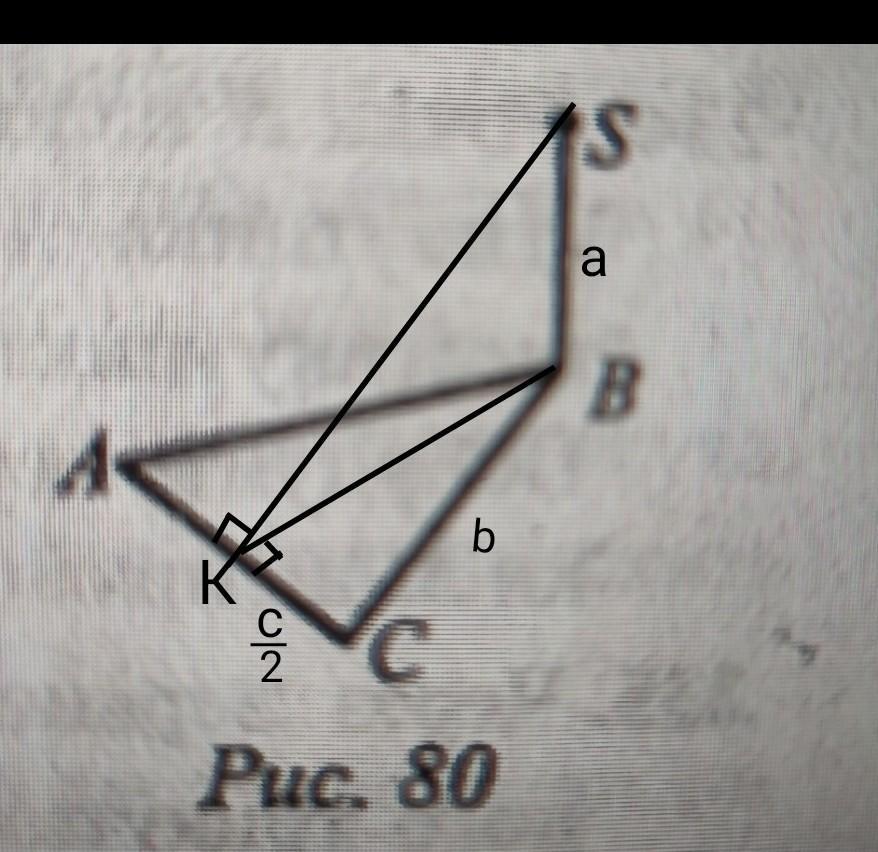
До площини рiвнобедреного трикутника АВС (AB = BC) провели перпендикуляр SB (рис. 80). Знайдіть відстань від точки S до прямої АС, якщо АС=с, ВС-b, SB-а.
Приложения:

Ответы
Автор ответа:
2
Ответ:
SK=√(4a²+4b²-c²)/2
Объяснение:
BK- висота, медіана і бісектриса рівнобедреного трикутника ∆АВС.
АК=КС, т.щ. ВК- медіана.
КС=АС/2=с/2.
∆ВКС- прямокутний трикутник
За теоремою Піфагора.
ВК²=ВС²-КС²=b²-(c/2)²=b²-c²/4=
=4b²/4-c²/4=(4b²-c²)/4
BK перпендикулярно АС, тоді SK перпендикулярно АС, за теоремою о трьох перпендикулярах.
∆SBK- прямокутний трикутник. (∠SBK=90°)
За теоремою Піфагора:
SK²=SB²+BK²=a²+(4b²-c²)/4=
=4a²/4+(4b²-c²)/4=(4a²+4b²-c²)/4
SK=√((4a²+4b²-c²)/4)=√(4a²+4b²-c²)/2
Приложения:
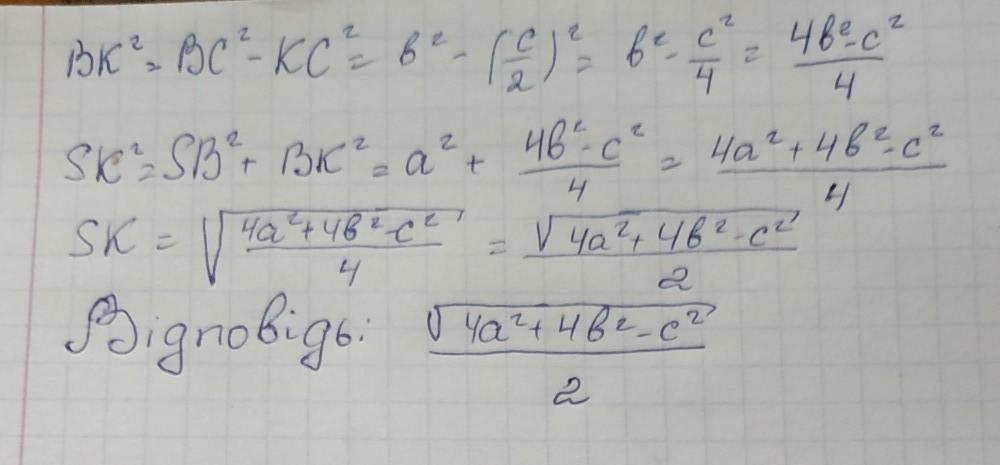
Похожие вопросы
Предмет: География,
автор: natashapetrik1995
Предмет: Другие предметы,
автор: nexst4824
Предмет: Қазақ тiлi,
автор: dinarakhairden
Предмет: Русский язык,
автор: Haliava228
Предмет: Математика,
автор: rewqqwer135