Предмет: Алгебра,
автор: inaraalekberova8683
Буду благодарна за решение данного дифференциала
Приложения:
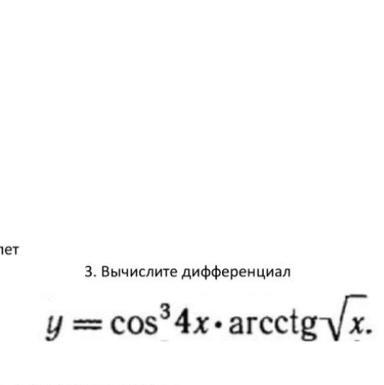
Ответы
Автор ответа:
1
Ответ:
Дифференциал функции вычисляем по формуле .
Производная произведения равна .
При нахождении производных сложных функций учитываем правило :
Похожие вопросы
Предмет: Английский язык,
автор: adrenalinka1909
Предмет: Английский язык,
автор: pasha8137
Предмет: Українська література,
автор: kryvoruka
Предмет: Геометрия,
автор: vetan2005
Предмет: Английский язык,
автор: GremmoryRias