Question

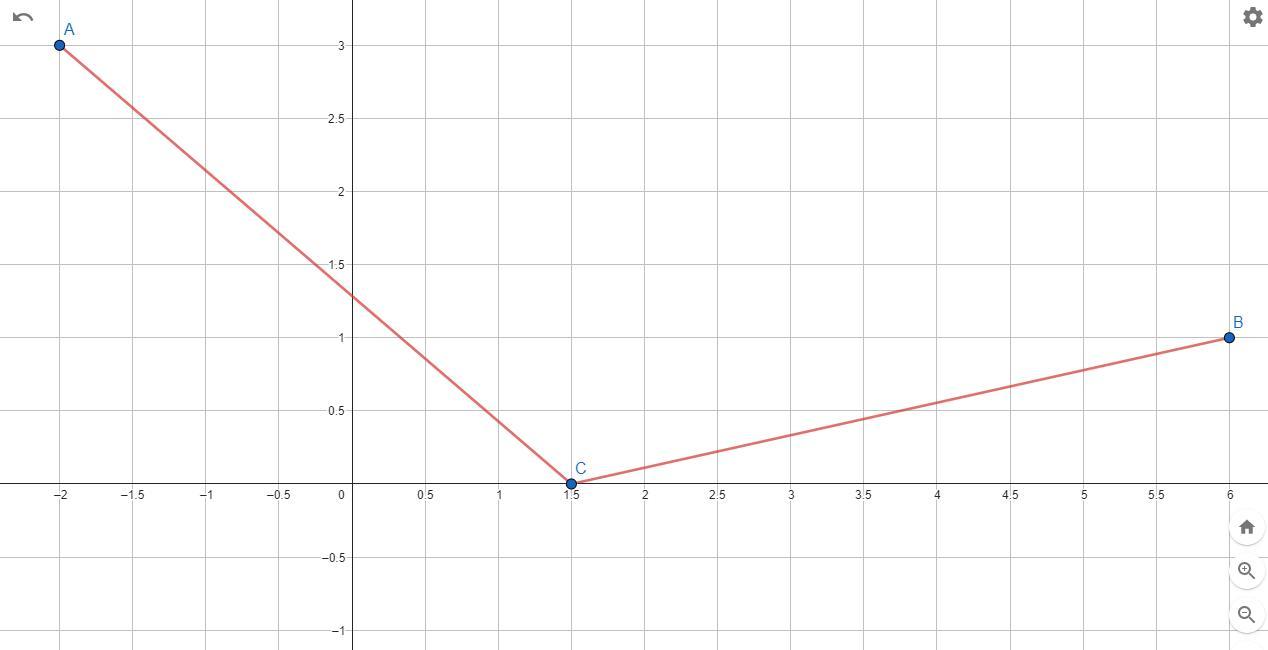
Найдите координаты точки, принадлежащей оси абсцесс и равноудалённой от точек А (-2; 3) и В (6; 1).​

Answer 1

Ответ: C( 1,5 ; 0)

Пошаговое объяснение:

Т.к  данная точка принадлежит оси абсцисс , то  ордината данной точки равна нулю

Другими словами , у нас имеется точка  C ( x , 0 )  которая равноудалена от точек   A(-2 ; 3)  и  B(6 ; 1)

Воспользуемся тем что  AC = BC

$AC =\sqrt{(-2 -x)^2 + (3-0)^2} = \sqrt{(x+2)^2 + 9 } \\\\ BC = \sqrt{(6-x)^2 + (1-0)^2} = \sqrt{(x-6)^2+1} \\\\ AB = BC \\\\ \sqrt{(x+2)^2 + 9} = \sqrt{(x-6)^2 +1} \\\\ (x+2)^2 + 9 = (x-6)^2 + 1 \\\\ (x-6)^2- (x+2)^2 = 8 \\\\ (x-6 -x -2)(x - 6 + x + 2) = 8 \\\\ -8 \cdot (2x -4) = 8 \\\\ 2x -4 = - 1 \\\\ x = 1,5$

По итогу наша точка имеет координаты   ( 1,5 ; 0)