Question

Пж помогиииите!!! Даю 100 бал. Только 2-ое задание!!!

Answer 1

Ответ:

Площадь фигуры F равна 4π см², длина линии, что ее ограничивает, равна 8π см.

Пошаговое объяснение:

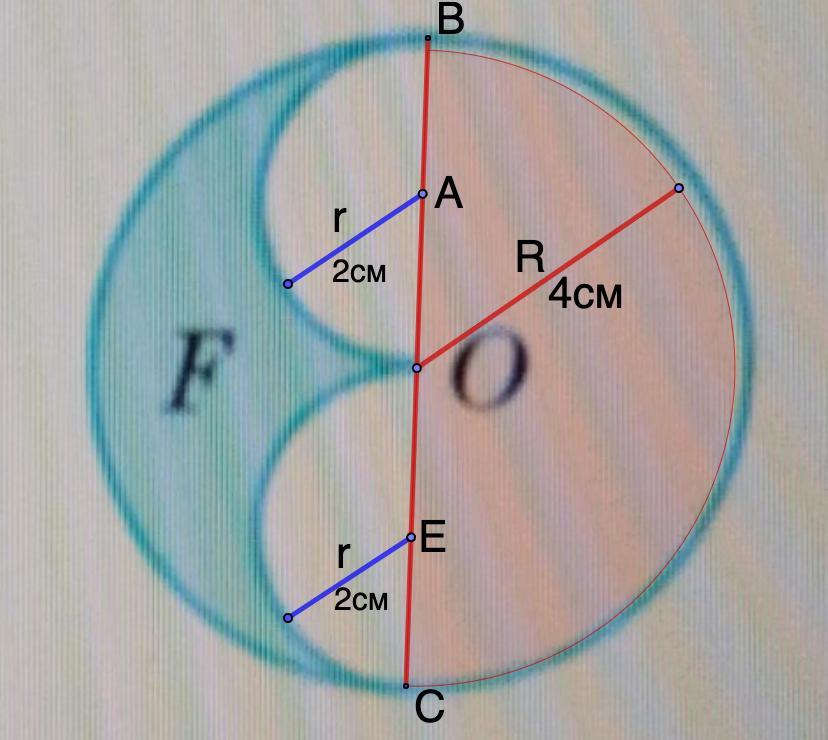
2. На рисунке закрашена фигуру F часть круга с центром в точке O и радиусом 4 см. Найдите площадь фигуры F и длину линии, что ее ограничивает.

Рассмотрим рисунок.

Фигура F ограничена слева полуокружностью радиуса R, справа - двумя полуокружностями радиуса r.

Формула площади круга:

S = πR²

Найдем площадь полукруга радиуса R.

S₁ = πR² : 2 = (π · 4²) : 2 = 8π (см²)

Найдем площади полукругов с центрами Е и А радиуса r.

Диаметры этих кругов равны радиусу круга с центром О.

• Радиус равен половине диаметра.

⇒ r = R : 2 = 4 : 2 = 2 (см²)

S₂ = S₃ = (πr²) : 2 = (π · 2²) : 2 = 2π (см²)

⇒ Площадь фигуры F равна:

S(F) = S₁ - (S₂ + S₃) = 8π - 2π - 2π = 4π (см²)

Площадь фигуры F равна 4π см².

Найдем длину линии, которая ограничивает фигуру F.

Формула длины окружности:

C = 2πR

⇒ Длина полуокружности равна πR.

Длина полуокружности с центром О:

С₁ = π · 4 = 4π (см)

Длина полуокружностей с центрами Е и А:

С₂ = С₃ = π · 2 = 2π (см)

Длина линии равна:

С(F) = C₁ + C₂ + C₃ = 4π + 2π + 2π = 8π (см)

Длина линии, которая ограничивает фигуру F, равна 8π см.