Предмет: Геометрия,
автор: olegharcmen
30 балов!!! вопрос в фото
Приложения:
Ответы
Автор ответа:
1
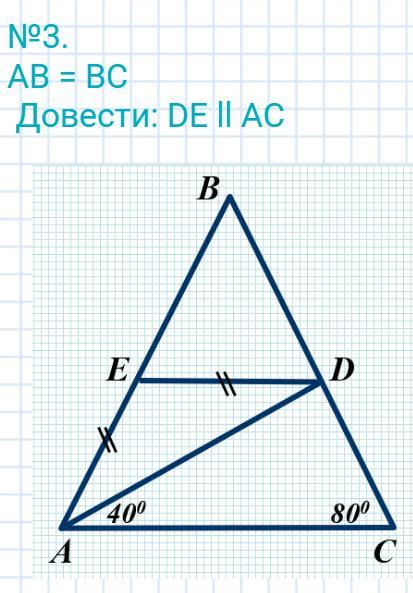
Ответ:
Доказано, что DE || AC.
Объяснение:
Требуется доказать, что DE || AC.
Дано: ΔАВС - равнобедренный, АВ = ВС;
ЕD = AE; ∠DAC = 40°; ∠C = 80°.
Доказать: DE || AC
Доказательство:
Отметим углы 1 и 2 (см. рис)
ΔАВС - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠С = ∠А = 80°
∠ 1 = ∠А - ∠DAC = 80° - 40° = 40°
ΔAED - равнобедренный (АЕ = ED)
⇒ ∠1 = ∠2 = 40° (при основании равнобедренного треугольника)
Получили ∠2 = ∠DAC = 40° (накрест лежащие при ED и АС и секущей AD)
- Если при пересечении двух прямых секущей накрест лежащие угла равны, то прямые параллельны.
⇒ ED || AC.
Приложения:

olegharcmen:
спасибо
можешь помоч в лс
Похожие вопросы
Предмет: Химия,
автор: sv2989491
Предмет: Биология,
автор: fligbom
Предмет: Математика,
автор: pipka7348
Предмет: Русский язык,
автор: gfjugbn
Предмет: Литература,
автор: Аноним