Предмет: Алгебра,
автор: milsonitos
2 задание 100 БАЛЛОВ СРОЧНО
Приложения:
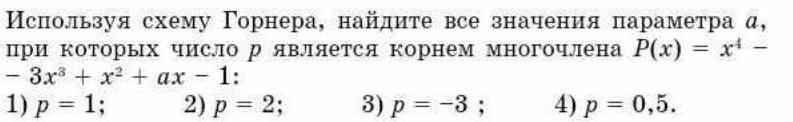
Ответы
Автор ответа:
1
Ответ:
1) a = 2
2) a = 2,5
3) a = 170/3
4) a = 2,125
Объяснение:
Используя схему Горнера , найдите все значения параметра a , при которых число p является корнем многочлена
P(x) = x⁴ - 3x³ + x² + ax - 1
1) p = 1
Т.к 1 является корнем данного уравнения , то
a - 2 = 0 ⇒ a = 2
2) p = 2
2a - 5 = 0 ⇒ a = 2,5
3) p = -3
4) p = 0,5
0,5a -1,0625 = 0 ⇒ a = 2,125
#SPJ1
tanktoonblitz:
а что означает cline 7?
Похожие вопросы
Предмет: Литература,
автор: lerakolodko534
Предмет: Українська мова,
автор: miroslavturkot4
Предмет: Українська мова,
автор: yanagydz777
Предмет: География,
автор: s628705
Предмет: История,
автор: oofgamer181144