Предмет: Геометрия,
автор: mariahrono97
Найти точку, удаленную на 5 единиц как от точки А(2; 1), так и от оси Оу.
Ответы
Автор ответа:
1
Ответ:
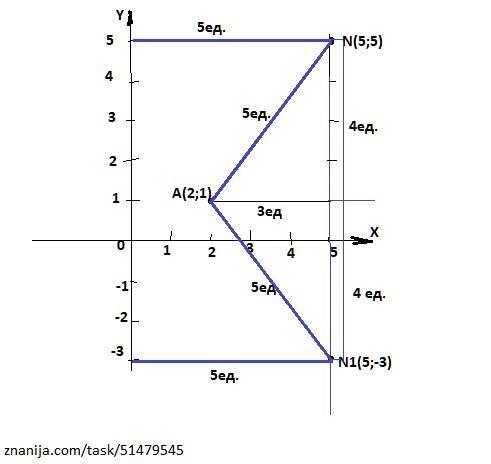
N(5;5). N1(5;-3).
Объяснение:
Искомая точка (точки) лежит на прямой, параллельной оси 0Y и удаленной от нее на расстоянии 5 единиц (дано). Следовательно, координата х этой точки (точек) равна 5.
Расстояние точки А от этой прямой равно 5 - 2 = 3 единицы.
Значит мы имеем прямоугольный треугольник с гипотенузой (расстояние от точки А до искомой точки), равной 5 единиц и катетом (расстояние от точки А до прямой), равным 3 единицы. Это пифагоров треугольник, второй катет которого равен 4 единицы.
Следовательно, координата Y искомой точки равна 4+1 = 5 или
4-1 =3 (1 - это координата Ay).
Значит искомых точек две: с координатами (5;5) и (5;-3).
Приложения:
Похожие вопросы
Предмет: Музыка,
автор: bombinanastia2018
Предмет: История,
автор: semenovvlad989
Предмет: Литература,
автор: m88262958
Предмет: Физика,
автор: Turboh
Предмет: Қазақ тiлi,
автор: 180619liza