Предмет: Математика,
автор: nikzed99
Найти границы функции .Расписать подробно
Приложения:
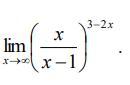
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Вычислить предел:
Для решения используем второй замечательный предел:
Преобразуем данное выражение под второй замечательный предел:
Так как → 0 при х → ∞, то
При этом
Искомый предел равен
Похожие вопросы
Предмет: Английский язык,
автор: xrebtovaso12
Предмет: История,
автор: housecompot
Предмет: История,
автор: alinkamalinkaalinka8
Предмет: Математика,
автор: zhukkseniya2007
Предмет: История,
автор: MafenJo