Question

Даю 70 баллoB
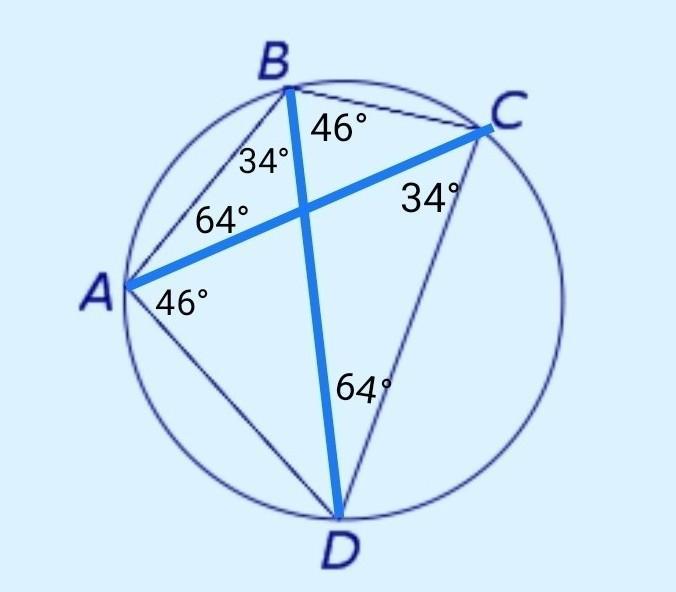
Найдите углы четырёхугольника ABCD , вписаного в окружность, если < CBD=46°,<ACD=34°, <BDC = 64°​

Answer 1

∠A = 110°;

∠B = 80°;

∠C = 70°;

∠D = 100°

1. Если четырёхугольник вписан в окружность, то образуются углы, вписанные в окружность. По теореме вписанный в окружность угол равен половине градусной меры дуги, на которую он опирается. Вписанные углы одной окружности, опирающиеся на одну и ту же дугу, равны.

В нашем случае

∠СВD = ∠CAD = 46°,

∠АСD = ∠ABD = 34°,

∠BDC = ∠BAC = 64°.

2. Получили, что

∠АВС = 34° + 46° = 80°;

∠ВАD = 64° + 46° = 110°.

3. По теореме, если четырёхугольник вписана а окружность, то суммы двух его противолежащих углов равны 180°, тогда

∠ADC = 180° - ∠ABC = 180° - 80° = 100°.

∠BCD = 180° - ∠BAD = 180° - 110° = 70°.

Итак, в четырёхугольнике ABCD

∠A = 110°;

∠B = 80°;

∠C = 70°;

∠D = 100°.