Предмет: Математика,
автор: filmorminecraft2288
Помощь даю 100 баллов!
Приложения:
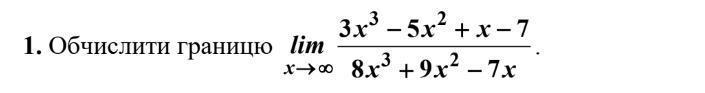
Ответы
Автор ответа:
2
Ответ:
3/8
Пошаговое объяснение:
При вычислении пределов с многочленами - легче числитель и знаменатель разделить почленно на х в старшой степени.
То есть:
Примечание:
Похожие вопросы
Предмет: Русский язык,
автор: ersagyn13
Предмет: Физика,
автор: bakugan0183
Предмет: Математика,
автор: alisahilevic97
Предмет: Музыка,
автор: Karishar
Предмет: Русский язык,
автор: pavelkorotun2005