Предмет: Математика,
автор: filmorminecraft2288
Помощь даю 100 баллов!
Приложения:
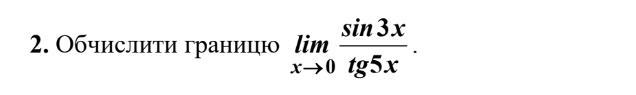
Ответы
Автор ответа:
2
Ответ:
3/5
Пошаговое объяснение:
Вспомним формулы:
_________________
Чтобы расскрыть данную неопределенность - воспользуемся правилом Лопиталя:
То есть:
Похожие вопросы
Предмет: Химия,
автор: l79797669
Предмет: Физика,
автор: bakugan0183
Предмет: Математика,
автор: kulmamax
Предмет: Математика,
автор: 707Nasny707
Предмет: Английский язык,
автор: dashadanich