Question

Основание пирамиды — ромб, узкий угол которого равен 30°. Высота пирамиды 3 √ 3. Все двугранные углы при основании пирамиды равны 60°. Вычислите длину ребра основания пирамиды.

Answer 1

Ответ:

12

Объяснение:

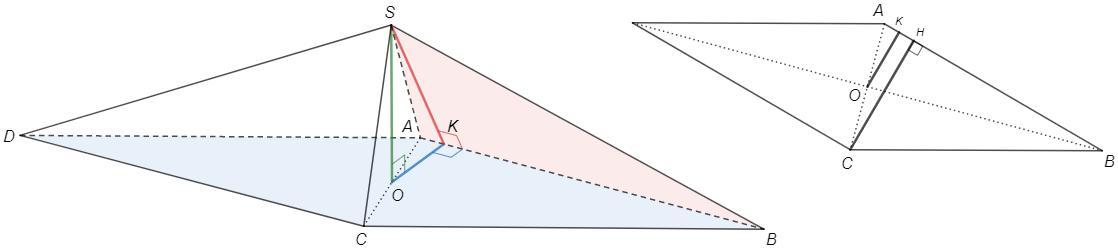
Опустим высоту пирамиды SO=3√3

Проведем перпендикуляр OK к ребру AB.

По т о трех перпендикулярах SK также перпендикуляр к AB

SO⊥ABC, OK⊥AB => SK⊥AB

Угол между плоскостями - угол между перпендикулярами к общей прямой.

∠(SABC)=∠SKO=60°

△SKO:   OK=SO/tg60° =3√3 :√3 =3

Если грани пирамиды наклонены к основанию под равными углами, то вершина пирамиды падает в центр вписанной окружности основания.

Центр вписанной окружности ромба - точка пересечения диагоналей.

Диагонали ромба точкой пересечения делятся пополам.

O - середина AC.

Проведем перпендикуляр CH к ребру AB.

CH||OK => CH=2OK =6

△BCH:   BC=CH/sin30° =6 :1/2 =12