Question

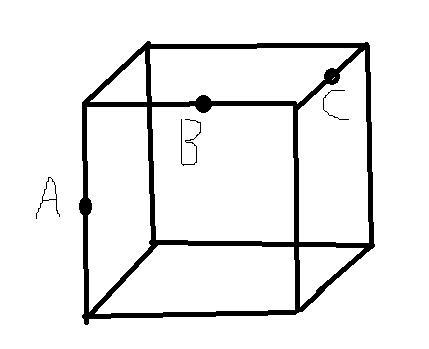
Дано куб. А, В и С - середины рёбер. Найти угол АВС

Answer 1

Ответ:

Угол АВС, образованный серединами трёх рёбер куба, равен 120°.

Объяснение:

Пусть длина ребра куба будет μ. DM = μ.

А, В и С - середины рёбер, поэтому МС = AD = BM = DB = μ/2.

Рассмотрим ΔDMC - прямоугольный.

DM = μ, MC = μ/2, по теореме Пифагора DC² = DM² + MC², поэтому:

$\displaystyle DC=\sqrt{DM^2+MC^2} = \sqrt{\mu^2+\bigg(\frac{\mu}{2}\bigg)^2 } =\sqrt{\frac{4\mu^2}{4}+\frac{\mu^2}{4} } =\sqrt{\frac{5\mu^2}{4} } =\frac{\mu\sqrt{5} }{2}$

DC = (μ√5)/2

Рассмотрим ΔADC - прямоугольный.

AD = μ/2, DC = (μ√5)/2, по теореме Пифагора АС² = AD² + DC², отсюда:

$\displaystyle AC^2= \sqrt{AD^2+DC^2} = \sqrt{\bigg(\frac{\mu}{2}\bigg)^2+ \bigg(\frac{\mu\sqrt{5} }{2}\bigg)^2} =\sqrt{\frac{\mu^2}{4} +\frac{5\mu^2}{4} } = \\\\ = \sqrt{\frac{6\mu^2}{4} } = \frac{\mu\sqrt{6} }{2}$

AC = (μ√6)/2

Рассмотрим ΔВМС - прямоугольный.

Имеем DB=DA=μ/2, по теореме Пифагора, АВ²=DB²+DA², тогда:

$\displaystyle AB = \sqrt{DB^2+DA^2} = \sqrt{\bigg(\frac{\mu}{2}\bigg)^2+\bigg(\frac{\mu}{2}\bigg)^2 } = \sqrt{2\cdot\bigg(\frac{\mu}{2}\bigg)^2} = \frac{\mu\sqrt{2} }{2}$

АВ = (μ√2)/2

Мы знаем, что DB=BM, AD=MC, треугольники - прямоугольные, поэтому ΔDBA=ΔMBC по двум катетам.

Из равенства треугольников имеем АВ=ВС=(μ√2)/2.

Рассмотрим ΔАВС - равнобедренный (АВ=ВС).

Проведём BH⊥AC.

Треугольник равнобедренный, поэтому BH - высота, медиана и б

ВН - медиана, поэтому АН = НС = 1/2АС = (μ√6)/4.

ВН - биссектриса, поэтому ∠АВН = ∠СВН = 1/2∠АВС.

Рассмотрим ΔВНС - прямоугольный.

Помним, что НС = (μ√6)/4 и ВС=(μ√2)/2, тогда:

$\displaystyle \sin \angle HBC = \frac{HC}{BC} = \frac{\mu\sqrt{6} }{4} \div \frac{\mu\sqrt{2} }{2} = \frac{\not\!\mu\sqrt{6} }{\not4} \cdot \frac{\not2}{\not\!\mu\sqrt{2} } =\frac{\sqrt{3}\cdot \not\!\!\!\!\!\sqrt{2} }{2\cdot \not\!\!\!\!\!\sqrt{2} } =\frac{\sqrt{3}}{2}$

∠HBC = arcsin(√3/2) = 60°

Знаем, что ∠СВН = 1/2∠АВС, тогда ∠АВС = 2∠СВН = 2 * 60° = 120°.

Угол АВС, образованный серединами трёх рёбер куба, равен 120°.