Предмет: Алгебра,
автор: karlygash1600
Найдите значение производной функции у = f(х) в точке х0
ПОМОГИТЕ ПОЖАЛУЙСТА НУЖНЫ ВСЕ 4 пожалуйста отдам все свои баллы
Приложения:
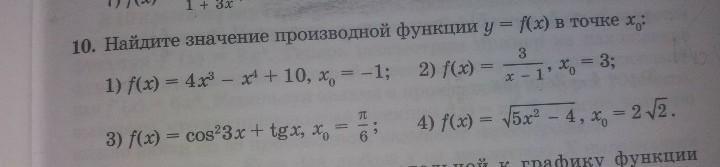
Ответы
Автор ответа:
3
Ответ:
1)16
2)-3/4
3)1 ⅓
4)(5√2)/3
Объяснение:
Вспомним формулу производной степенной функции и константы:
И тогда мы получим:
Производная в точке х₀ = -1:
Из формулы производной дроби:
Следует:
Производная в точке x₀ = 3:
Тут уже по правилу производной сложной функции:
Ещё с учётом того , что производная от суммы равна производной от каждого слагаемого:
В точке x₀ = π/6:
По формуле:
И по правилу производной сложной функции мы получим:
В точке x₀ = 2√2:
Похожие вопросы
Предмет: Английский язык,
автор: snicukdasa
Предмет: Русский язык,
автор: bletfikus1
Предмет: География,
автор: k97099221
Предмет: Физика,
автор: Aruzhan160103
Предмет: Английский язык,
автор: haah92